Differential Geometry of Generative Models
A lot of recent research in the field of generative models has focused on the geometry of the learned latent space (see the references at the end of this section for examples). The non-linear nature of neural networks makes it relevant to consider the non-Euclidean geometry of the latent space when trying to gain insights into the structure of the learned space. In other words, given that neural networks involve a series of non-linear transformations of the input data, we cannot expect the latent space to be Euclidean, and thus, we need to account for curvature and other non-Euclidean properties. For this, we can borrow concepts and tools from Riemannian geometry, now applied to the latent space of generative models.
AutoEncoderToolkit.jl aims to provide the set of necessary tools to study the geometry of the latent space in the context of variational autoencoders generative models.
This is very much work in progress. As always, contributions are welcome!
A word on Riemannian geometry
In what follows we will give a very short primer on some relevant concepts in differential geometry. This includes some basic definitions and concepts along with what we consider intuitive explanations of the concepts. We trade rigor for accessibility, so if you are looking for a more formal treatment, this is not the place.
These notes are partially based on the 2022 paper by Chadebec et al. [2].
A $d$-dimensional manifold $\mathcal{M}$ is a manifold that is locally homeomorphic to a $d$-dimensional Euclidean space. This means that the manifold–some surface or high-dimensional shape–when observed from really close, can be stretched or bent without tearing or gluing it to make it resemble regular Euclidean space.
If the manifold is differentiable, it possesses a tangent space $T_z$ at any point $z \in \mathcal{M}$ composed of the tangent vectors of the curves passing by $z$.
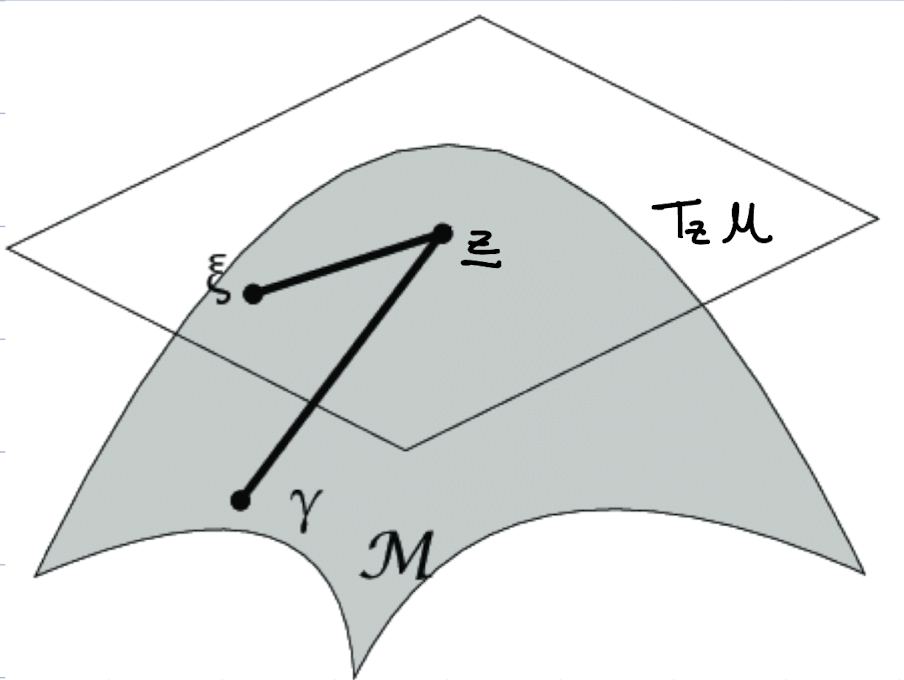
If the manifold $\mathcal{M}$ is equipped with a smooth inner product,
\[g: z \rightarrow \langle \cdot \mid \cdot \rangle_z, \tag{1}\]
defined on the tangent space $T_z$ for any $z \in \mathcal{M}$, then $\mathcal{M}$ is a Riemannian manifold and $g$ is the associated Riemannian metric. With this, a local representation of $g$ at any point $z$ is given by the positive definite matrix $\mathbf{G}(z)$.
A chart (fancy name for a coordinate system) $(U, \phi)$ provides a homeomorphic mapping between an open set $U$ of the manifold and an open set $V$ of Euclidean space. This means that there is a way to bend and stretch any segment of the manifold to make it look like a segment of Euclidean space. Therefore, given a point $z \in U$, a chart–its coordinate–$\phi: (z_1, z_2, \ldots, z_d)$ induces a basis $\{\partial_{z_1}, \partial_{z_2}, \ldots, \partial_{z_d}\}$ on the tangent space $T_z \mathcal{M}$. In other words, the partial derivatives of the manifold with respect to the dimensions form a basis (think of $\hat{i}, \hat{j}, \hat{k}$ in 3D space) for the tangent space at that point. Hence, the metric–a "position-dependent scale-bar"–of a Riemannian manifold can be locally represented at $\phi$ as a positive definite matrix $\mathbf{G}(z)$ with components $g_{ij}(z)$ of the form
\[g_{ij}(z) = \langle \partial_{z_i} \mid \partial_{z_j} \rangle_z. \tag{2}\]
This implies that for every pair of vectors $v, w \in T_z \mathcal{M}$ and a point $z \in \mathcal{M}$, the inner product $\langle v \mid w \rangle_z$ is given by
\[\langle v \mid w \rangle_z = v^T \mathbf{G}(z) w. \tag{3}\]
If $\mathcal{M}$ is connected–a continuous shape with no breaks–a Riemannian distance between two points $z_1, z_2 \in \mathcal{M}$ can be defined as
\[\text{dist}(z_1, z_2) = \min_{\gamma} \int_0^1 dt \sqrt{\langle \dot{\gamma}(t) \mid \dot{\gamma}(t) \rangle_{\gamma(t)}}, \tag{4}\]
where $\gamma$ is a 1D curve traveling from $z_1$ to $z_2$, i.e., $\gamma(0) = z_1$ and $\gamma(1) = z_2$. Another way to state this is that the length of a curve on the manifold $\gamma$ is given by
\[L(\gamma) = \int_0^1 dt \sqrt{\langle \dot{\gamma}(t) \mid \dot{\gamma}(t) \rangle_{\gamma(t)}}. \tag{5}\]
If $L$ minimizes the distance between the initial and final points, then $\gamma$ is a geodesic curve.
The concept of geodesic is so important the study of the Riemannian manifold learned by generative models that let's try to give another intuitive explanation. Let us consider a curve $\gamma$ such that
\[\gamma: [0, 1] \rightarrow \mathbb{R}^d, \tag{6}\]
In words, $\gamma$ is a function that, without loss of generality, maps a number between zero and one to the dimensionality of the latent space (the dimensionality of our manifold). Let us define $f$ to be a continuous function that embeds any point along the curve $\gamma$ into the data space, i.e.,
\[f : \gamma(t) \rightarrow x \in \mathbb{R}^n. \tag{7}\]
where $n$ is the dimensionality of the data space.
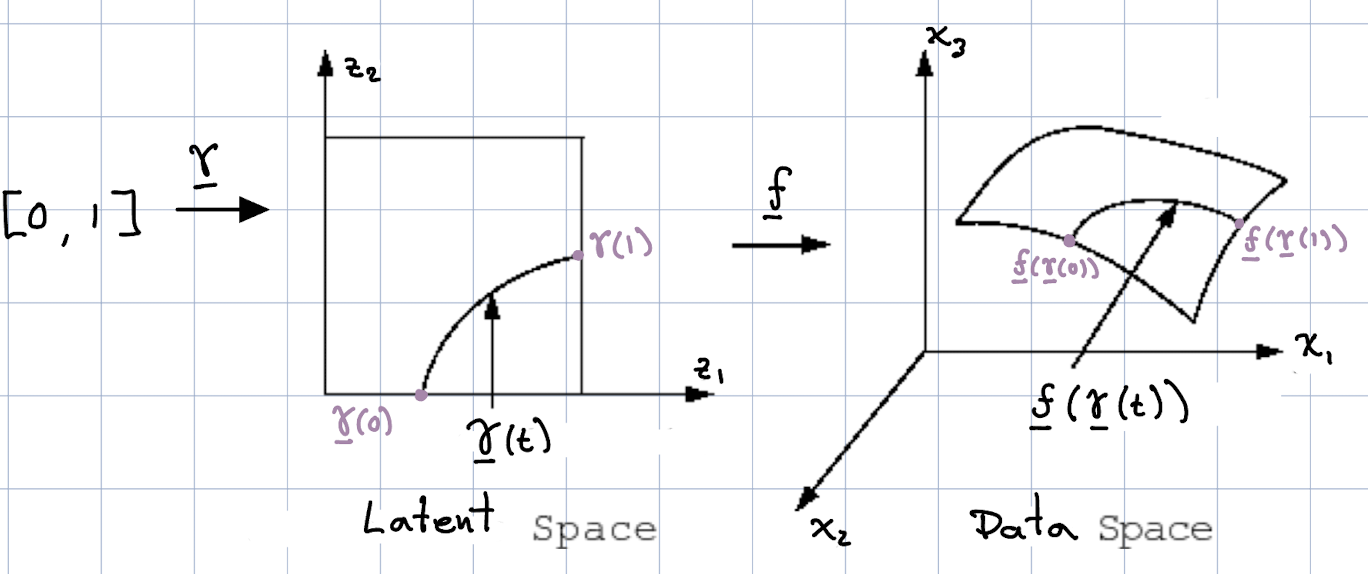
The length of this curve in the data space is given by
\[L(\gamma) = \int_0^1 dt \left\| \frac{d f}{dt} \right\|_2. \tag{8}\]
After some manipulation, we can show that the length of the curve in the data space is given by
\[L(\gamma) = \int_0^1 dt \sqrt{ \dot{\gamma}(t)^T \mathbf{G}(\gamma(t)) \dot{\gamma}(t) }, \tag{9}\]
where $\dot{\gamma}(t)$ is the derivative of $\gamma$ with respect to $t$, and $T$ denotes the transpose of a vector. For a Euclidean space, the length of the curve would take the same functional form, except that the metric tensor would be given by the identity matrix. This is why the metric tensor can be thought of as a position-dependent scale-bar.
Neural Geodesic Networks
Computing a geodesic on a Riemannian manifold is a non-trivial task, especially when the manifold is parametrized by a neural network. Thus, knowing the function $\gamma$ that minimizes the distance between two points $z_1$ and $z_2$ is not straightforward. However, as first suggested by Chen et al. [1], we can repurpose the expressivity of neural networks to approximate almost any function to approximate the geodesic curve. This is the idea behind the Neural Geodesic module in AutoEncoderToolkit.jl.
Briefly, to approximate the geodesic curve between two points $z_1$ and $z_2$ in latent space, we define a neural network $g_\omega$ such that
\[g_\omega: \mathbb{R} \rightarrow \mathbb{R}^d, \tag{10}\]
i.e., the neural network takes a number between zero and one and maps it to the dimensionality of the latent space. The intention is to have $g_\omega \approx \gamma$, where $\omega$ are the parameters of the neural network we are free to optimize.
We approximate the integral defining the length of the curve in the latent space with $n$ equidistantly sampled points $t_i$ between zero and one. The length of the curve is then approximated by
\[L(g_\gamma(t)) \approx \frac{1}{n} \sum_{i=1}^n \sqrt{ \dot{g}_\omega(t_i)^T \mathbf{G}(g_\omega(t_i)) \dot{g}_\omega(t_i) },\]
By setting the loss function to be this approximation of the length of the curve, we can train the neural network to approximate the geodesic curve.
AutoEncoderToolkit.jl provides the NeuralGeodesic struct to implement this idea. The struct takes three inputs:
- The multi-layer perceptron (MLP) that approximates the geodesic curve.
- The initial point in latent space.
- The final point in latent space.
NeuralGeodesic struct
AutoEncoderToolkit.diffgeo.NeuralGeodesics.NeuralGeodesic — TypeNeuralGeodesicType to define a neural network that approximates a geodesic curve on a Riemanian manifold. If a curve γ̲(t) represents a geodesic curve on a manifold, i.e.,
L(γ̲) = min_γ ∫ dt √(⟨γ̲̇(t), M̲̲ γ̲̇(t)⟩),where M̲̲ is the Riemmanian metric, then this type defines a neural network g_ω(t) such that
γ̲(t) ≈ g_ω(t).This neural network must have a single input (1D). The dimensionality of the output must match the dimensionality of the manifold.
Fields
mlp::Flux.Chain: Neural network that approximates the geodesic curve. The dimensionality of the input must be one.z_init::AbstractVector: Initial position of the geodesic curve on the latent space.z_end::AbstractVector: Final position of the geodesic curve on the latent space.
Citation
Chen, N. et al. Metrics for Deep Generative Models. in Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics 1540–1550 (PMLR, 2018).
NeuralGeodesic forward pass
AutoEncoderToolkit.diffgeo.NeuralGeodesics.NeuralGeodesic — Method (g::NeuralGeodesic)(t::AbstractArray)Computes the output of the NeuralGeodesic at each given time in t by scaling and shifting the output of the neural network.
Arguments
t::AbstractArray: An array of times at which the output of the NeuralGeodesic is to be computed. This must be within the interval [0, 1].
Returns
output::Array: The computed output of the NeuralGeodesic at each time int.
Description
The function computes the output of the NeuralGeodesic at each given time in t. The steps are:
- Compute the output of the neural network at each time in
t. - Compute the output of the neural network at time 0 and 1.
- Compute scale and shift parameters based on the initial and end points of the geodesic and the neural network outputs at times 0 and 1.
- Scale and shift the output of the neural network at each time in
taccording to these parameters. The result is the output of the NeuralGeodesic at each time int.
Scale and shift parameters are defined as:
- scale = (zinit - zend) / (ẑinit - ẑend)
- shift = (zinit * ẑend - zend * ẑinit) / (ẑinit - ẑend)
where zinit and zend are the initial and end points of the geodesic, and ẑinit and ẑend are the outputs of the neural network at times 0 and 1, respectively.
Note
Ensure that each t in the array is within the interval [0, 1].
NeuralGeodesic loss function
AutoEncoderToolkit.diffgeo.NeuralGeodesics.loss — Functionloss(
curve::NeuralGeodesic,
rhvae::RHVAE,
t::AbstractVector;
curve_velocity::Function=curve_velocity_TaylorDiff,
curve_integral::Function=curve_length,
)Function to compute the loss for a given curve on a Riemmanian manifold. The loss is defined as the integral over the curve, computed using the provided curve_integral function (either length or energy).
Arguments
curve::NeuralGeodesic: The curve on the Riemmanian manifold.rhvae::RHVAE: The Riemmanian Hamiltonian Variational AutoEncoder used to compute the Riemmanian metric tensor.t::AbstractVector: Vector of time points at which the curve is sampled.
Optional Keyword Arguments
curve_velocity::Function=curve_velocity_TaylorDiff: Function to compute the velocity of the curve. Default iscurve_velocity_TaylorDiff. Also acceptscurve_velocity_finitediff.curve_integral::Function=curve_length: Function to compute the integral over the curve. Default iscurve_energy. Also acceptscurve_length.
Returns
Loss::Number: The computed loss for the given curve.
Notes
This function first computes the geodesic curve using the provided curve function. It then computes the Riemmanian metric tensor using the metric_tensor function from the RHVAE module with the computed curve and the provided rhvae. The velocity of the curve is then computed using the provided curve_velocity function. Finally, the integral over the curve is computed using the provided curve_integral function and returned as the loss.
NeuralGeodesic training
AutoEncoderToolkit.diffgeo.NeuralGeodesics.train! — Functiontrain!(
curve::NeuralGeodesic,
rhvae::RHVAE,
t::AbstractVector,
opt::NamedTuple;
loss::Function=loss,
loss_kwargs::NamedTuple=NamedTuple(),
verbose::Bool=false,
loss_return::Bool=false,
)Function to train a NeuralGeodesic model using a Riemmanian Hamiltonian Variational AutoEncoder (RHVAE). The training process involves computing the gradient of the loss function and updating the model parameters accordingly.
Arguments
curve::NeuralGeodesic: The curve on the Riemmanian manifold.rhvae::RHVAE: The Riemmanian Hamiltonian Variational AutoEncoder used to compute the Riemmanian metric tensor.t::AbstractVector: Vector of time points at which the curve is sampled. These must be equally spaced.opt::NamedTuple: The optimization parameters.
Optional Keyword Arguments
loss_function::Function=loss: The loss function to be minimized during training. Default isloss.loss_kwargs::NamedTuple=NamedTuple(): Additional keyword arguments to be passed to the loss function.verbose::Bool=false: Iftrue, the loss value is printed at each iteration.loss_return::Bool=false: Iftrue, the function returns the loss value.
Returns
Loss::Number: The computed loss for the given curve. This is only returned ifloss_returnistrue.
Notes
This function first computes the gradient of the loss function with respect to the model parameters. It then updates the model parameters using the computed gradient and the provided optimization parameters. If verbose is true, the loss value is printed at each iteration. If loss_return is true, the function returns the loss value.
Other functions for NeuralGeodesic
AutoEncoderToolkit.diffgeo.NeuralGeodesics.curve_velocity_TaylorDiff — Functioncurve_velocity_TaylorDiff(
curve::NeuralGeodesic,
t
)Compute the velocity of a neural geodesic curve at a given time using Taylor differentiation.
This function takes a NeuralGeodesic instance and a time t, and computes the velocity of the curve at that time using Taylor differentiation. The computation is performed for each dimension of the latent space.
Arguments
curve::NeuralGeodesic: The neural geodesic curve.t: The time at which to compute the velocity.
Returns
A vector representing the velocity of the curve at time t.
Notes
This function uses the TaylorDiff package to compute derivatives. Please note that TaylorDiff has limited support for certain activation functions. If you encounter an error while using this function, it may be due to the activation function used in your NeuralGeodesic instance.
curve_velocity_TaylorDiff(
curve::NeuralGeodesic,
t::AbstractVector
)Compute the velocity of a neural geodesic curve at each time in a vector of times using Taylor differentiation.
This function takes a NeuralGeodesic instance and a vector of times t, and computes the velocity of the curve at each time using Taylor differentiation. The computation is performed for each dimension of the latent space and each time in t.
Arguments
curve::NeuralGeodesic: The neural geodesic curve.t::AbstractVector: The vector of times at which to compute the velocity.
Returns
A matrix where each column represents the velocity of the curve at a time in t.
Notes
This function uses the TaylorDiff package to compute derivatives. Please note that TaylorDiff has limited support for certain activation functions. If you encounter an error while using this function, it may be due to the activation function used in your NeuralGeodesic instance.
AutoEncoderToolkit.diffgeo.NeuralGeodesics.curve_velocity_finitediff — Functioncurve_velocity_finitediff(
curve::NeuralGeodesic,
t::AbstractVector;
fdtype::Symbol=:central,
)Compute the velocity of a neural geodesic curve at each time in a vector of times using finite difference methods.
This function takes a NeuralGeodesic instance, a vector of times t, and an optional finite difference type fdtype (which can be either :forward or :central), and computes the velocity of the curve at each time using the specified finite difference method. The computation is performed for each dimension of the latent space and each time in t.
Arguments
curve::NeuralGeodesic: The neural geodesic curve.t::AbstractVector: The vector of times at which to compute the velocity.fdtype::Symbol=:central: The type of finite difference method to use. Can be either:forwardor:central. Default is:central.
Returns
A matrix where each column represents the velocity of the curve at a time in t.
Notes
This function uses finite difference methods to compute derivatives. Please note that the accuracy of the computed velocities depends on the chosen finite difference method and the step size used, which is determined by the machine epsilon of the type of t.
AutoEncoderToolkit.diffgeo.NeuralGeodesics.curve_length — Functioncurve_length(
riemannian_metric::AbstractArray,
curve_velocity::AbstractArray,
t::AbstractVector;
)Function to compute the (discretized) integral defining the length of a curve γ̲ on a Riemmanina manifold. The length is defined as
L(γ̲) = ∫ dt √(⟨γ̲̇(t), G̲̲ γ̲̇(t)⟩),where γ̲̇(t) defines the velocity of the parametric curve, and G̲̲ is the Riemmanian metric tensor. For this function, we approximate the integral as
L(γ̲) ≈ ∑ᵢ Δt √(⟨γ̲̇(tᵢ)ᵀ G̲̲ (γ̲(tᵢ+1)) γ̲̇(tᵢ))⟩),where Δt is the time step between points. Note that this Δt is assumed to be constant, thus, the time points t must be equally spaced.
Arguments
riemannian_metric::AbstractArray:d×d×Ntensor wheredis the dimension of the manifold on which the curve lies andNis the number of sampled time points along the curve. Each slice of the array represents the Riemmanian metric tensor for the curve at the corresponding time point.curve_velocity::AbstractArray:d×NMatrix wheredis the dimension of the manifold on which the curve lies andNis the number of sampled time points along the curve. Each column represents the velocity of the curve at the corresponding time point.t::AbstractVector: Vector of time points at which the curve is sampled.
Returns
Length::Number: Approximation of the Length for the path on the manifold.
AutoEncoderToolkit.diffgeo.NeuralGeodesics.curve_energy — Functioncurve_energy(
riemannian_metric::AbstractArray,
curve_velocity::AbstractArray,
t::AbstractVector;
)Function to compute the (discretized) integral defining the energy of a curve γ̲ on a Riemmanina manifold. The energy is defined as
E(γ̲) = ∫ dt ⟨γ̲̇(t), G̲̲ γ̲̇(t)⟩,where γ̲̇(t) defines the velocity of the parametric curve, and G̲̲ is the Riemmanian metric tensor. For this function, we approximate the integral as
E(γ̲) ≈ ∑ᵢ Δt ⟨γ̲̇(tᵢ)ᵀ G̲̲ (γ̲(tᵢ+1) γ̲̇(tᵢ))⟩,where Δt is the time step between points. Note that this Δt is assumed to be constant, thus, the time points t must be equally spaced.
Arguments
riemannian_metric::AbstractArray:d×d×Ntensor wheredis the dimension of the manifold on which the curve lies andNis the number of sampled time points along the curve. Each slice of the array represents the Riemmanian metric tensor for the curve at the corresponding time point.curve_velocity::AbstractArray:d×NMatrix wheredis the dimension of the manifold on which the curve lies andNis the number of sampled time points along the curve. Each column represents the velocity of the curve at the corresponding time point.t::AbstractVector: Vector of time points at which the curve is sampled.
Returns
Energy::Number: Approximation of the Energy for the path on the manifold.
References
- Chen, N. et al. Metrics for Deep Generative Models. in Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics 1540–1550 (PMLR, 2018).
- Chadebec, C. & Allassonnière, S. A Geometric Perspective on Variational Autoencoders. Preprint at http://arxiv.org/abs/2209.07370 (2022).
- Chadebec, C., Mantoux, C. & Allassonnière, S. Geometry-Aware Hamiltonian Variational Auto-Encoder. Preprint at http://arxiv.org/abs/2010.11518 (2020).
- Arvanitidis, G., Hauberg, S., Hennig, P. & Schober, M. Fast and Robust Shortest Paths on Manifolds Learned from Data. in Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics 1506–1515 (PMLR, 2019).
- Arvanitidis, G., Hauberg, S. & Schölkopf, B. Geometrically Enriched Latent Spaces. Preprint at https://doi.org/10.48550/arXiv.2008.00565 (2020).
- Arvanitidis, G., González-Duque, M., Pouplin, A., Kalatzis, D. & Hauberg, S. Pulling back information geometry. Preprint at http://arxiv.org/abs/2106.05367 (2022).
- Fröhlich, C., Gessner, A., Hennig, P., Schölkopf, B. & Arvanitidis, G. Bayesian Quadrature on Riemannian Data Manifolds.
- Kalatzis, D., Eklund, D., Arvanitidis, G. & Hauberg, S. Variational Autoencoders with Riemannian Brownian Motion Priors. Preprint at http://arxiv.org/abs/2002.05227 (2020).
- Arvanitidis, G., Hansen, L. K. & Hauberg, S. Latent Space Oddity: on the Curvature of Deep Generative Models. Preprint at http://arxiv.org/abs/1710.11379 (2021).