Development Log
All the workflows here is not restricted to one type of model output. After being familiar with new ideas and new models, one can easily make use of existing samples and create reader of their own. Because of the embarrassing parallelism nature of postprocessing, it is quite easy to take advantage of parallel approaches to process the data.
For the plotting, streamline tracing and particle tracing, a common problem is the grid and related interpolation process. Now I have FieldTracer.jl and TestParticle.jl designed specifically for these tasks.
Test Data
If you don't have SWMF data at hand, Batsrus.jl provides some test data for you to begin with.
using LazyArtifacts
datapath = artifact"testdata" # where you can find multiple test data filesThese are also used in the standard test. These will be automatically downloaded from batsrus_data if you run the package test locally.
VTK AMR Grid Structure
vtkOverlappingAMR implements a somewhat strict Berger-Collela AMR scheme:
- All grids are Cartesian.
- Grids at the same level do not overlap.
- The refinement ratios, RL, between adjacent levels are integer (typically 2 or 4) and uniform within the same level.
- Grid cells are never partially refined; i.e., each cell is refined to four quads in 2D or eight hexahedra in 3D.
Or in other words,
- Refinement ratio across levels is constant.
- Each block at levels > 0 need to be covered 100% by one parent block of
previous level.
- Some other restriction about what happens at the boundary.
You can directly use vtkUniformGridAMR, which does not impose any restrictions. Most filters should work for this class - there just wouldn't be any specialized filters such as the dual-grid contour / clip ones for the vtkOverlappingAMR.
The vtkAMRInformation documentation consists only of
- Refinement ratio between AMR levels
- Grid spacing for each level
- The file block index for each block parent child information, if requested
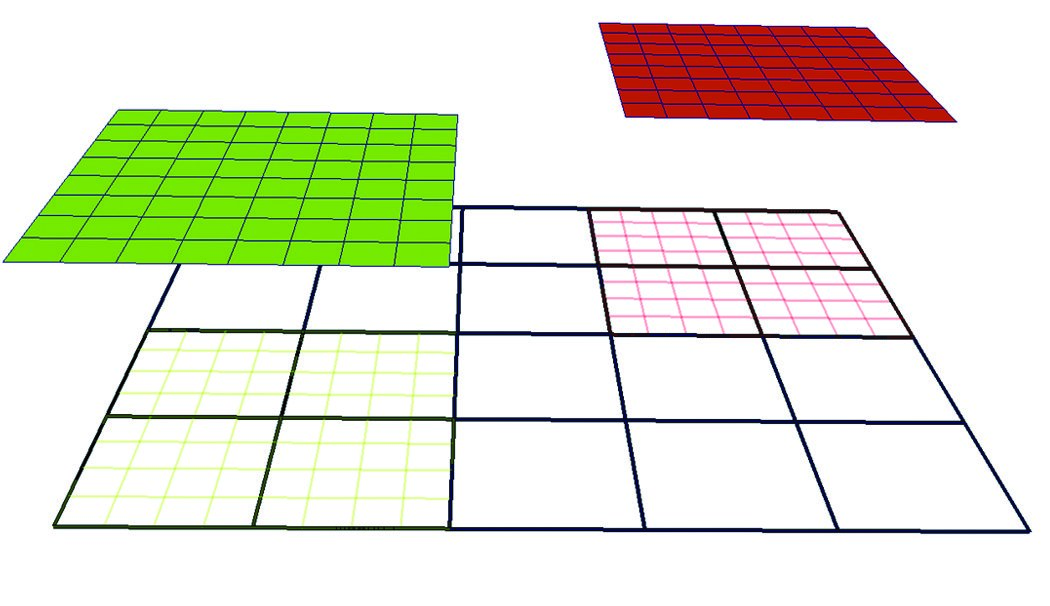 Sample 2D AMR Dataset with two levels and refinement ratio, RL=4. The root level (L0) consists of a single grid shown in black wireframe while the next level (L1) consists of two grids, depicted in green wireframe and red wireframe respectively. The two grids at L1 are projected from the root level to illustrate that the cells underneath are “hidden.”
Sample 2D AMR Dataset with two levels and refinement ratio, RL=4. The root level (L0) consists of a single grid shown in black wireframe while the next level (L1) consists of two grids, depicted in green wireframe and red wireframe respectively. The two grids at L1 are projected from the root level to illustrate that the cells underneath are “hidden.”
In VTK, the collection of AMR grids is stored in a vtkHierarchicalBoxDataSet data-structure. Each grid, G(Li,k), is represented by a vtkUniformGrid data structure where the unique key pair (Li,k) denotes the corresponding level (Li) and the grid index within the level (k) with respect to the underlying hierarchical structure. An array historically known as IBLANK, stored as a cell attribute in vtkUniformGrid, denotes whether a cell is hidden or not. The blanking array is subsequently used by the mapper to hide lower resolution cells accordingly when visualizing the dataset.
To enable the execution of data queries without loading the entire dataset in memory, metadata information is employed. The metadata stores a minimal set of geometric information for each grid in the AMR hierarchy. Specifically, the AMR metadata, B(Li,k), corresponding to the grid G(Li,k), is represented using a vtkAMRBox object and it consists of the following information:
- N={Nx, Ny, Nz} — the cell dimensions of the grid (since the data is cell-centered)
- The grid spacing at level L, hL={hx,hy,hz}
- The grid level Li and grid index k
- The global dataset origin, X=(X0, Y0, Z0), i.e., the minimum origin from all grids in level L0
- The LoCorner and HiCorner, which describe the low and high corners of the rectangular region covered by the corresponding grid in a virtual integer lattice with the same spacing (h) that covers the entire domain.
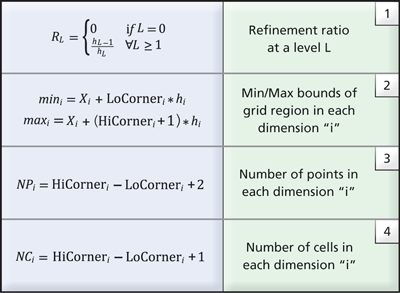
Given the metadata information stored in the AMR box of each grid, the refinement ratio at each level can be easily computed using relationship (1) from Table 1. Further, the cartesian bounds the corresponding grid covers and the number of points and cells is also available (see relationships 2-4 in Table 1). Notably, geometric queries such as determining which cell contains a given point, or if a grid intersects a user-supplied slice plane, can be answered using just the metadata.
There is a vtkAMRDualExtractionFilter, which constructs a dual-mesh (i.e., the mesh constructed by connecting the cell-centers) over the computational domain. If we can directly tell ParaView that the mesh we have is a dual-mesh, then the initial trial with multi-block data may work directly.
AMRGaussianPulseSource
See Multi-Resolution Rendering with Overlapping AMR for the implementation of C++ reader in VTK.