BioCCP.jl : Collecting Coupons in combinatorial biotechnology

Intro

During the combinatorial engineering of biosystems such as proteins, genetic circuits and genomes, diverse libraries are generated by assembling and recombining modules. The variants with the optimal phenotypes are selected with screening techniques. However, when the number of available modules to compose biological designs increases, a combinatorial explosion of design possibilities arises, allowing only for a part of the libary to be analyzed. In this case, it is important for a researcher to get insight in which (minimum) sample size sufficiently covers the design space, i.e. what is the expected minimum number of designs so that all modules are observed at least once.

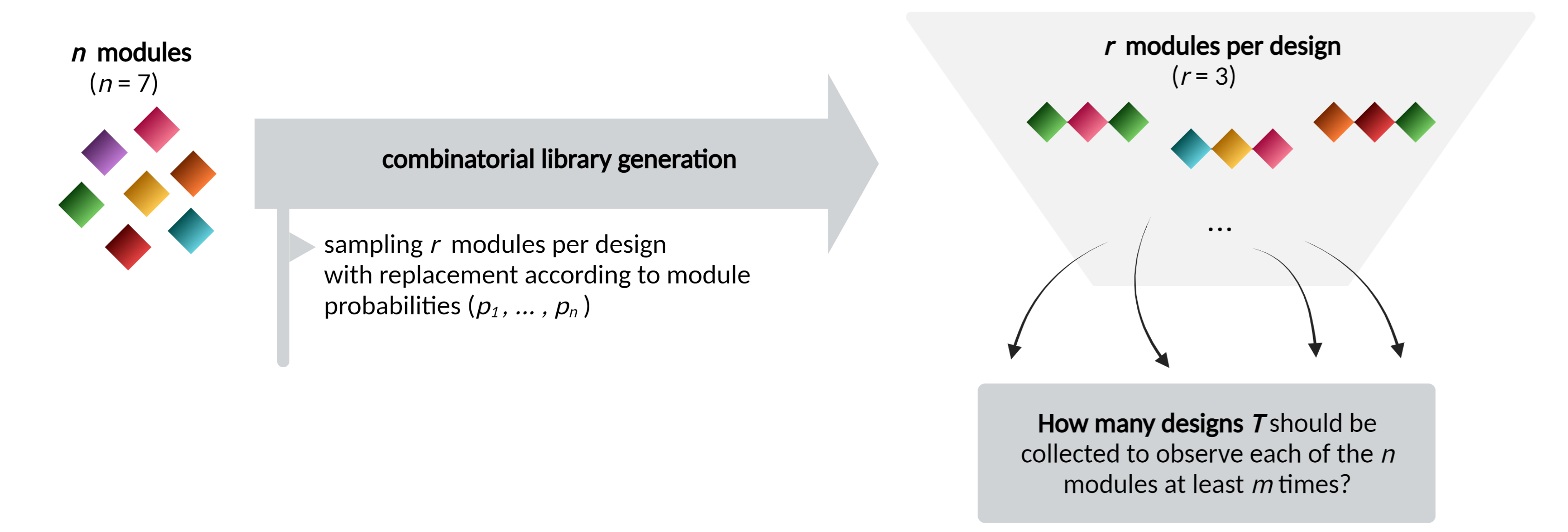
Functions

BioCCP contains functions for calculating (expected) minimum sample sizes and related statistics:

Function name	Short description
`expectation_minsamplesize`	Calculates the expected minimum number of designs to observe all modules at least m times
`std_minsamplesize`	Calculates standard deviation on the minimum number of designs
`success_probability`	Calculates the probability that the minimum number of designs T is smaller than or equal to a given sample size t
`expectation_fraction_collected`	Returns the fraction of the total number of modules in the design space that is expected to be observed for a given sample size t
`prob_occurrence_module`	Calculates for a module with specified module probability p, the probability that the module has occurred k times when a given number of designs has been collected

For more info about the implementation of the functions, please consult the docs or source code.

Pluto notebooks

1. Report-generating Pluto notebook

The first Pluto notebook provides an interactive illustration of all functions in BioCCP and assembles a report for your specific design set-up.

Inputs

Symbol	Short description
n	Total number of modules in the design space
r	The number of modules per design
m	The number of times each module has to be observed (default = 1) in the sampled set of designs
p (*)	Probability distribution of the modules

(*) When exact probabilities are known, define your custom module probability/abundance vector or load them in the notebook from an external file. When probabilities and/or their distribution are unknown, you can either:

Assume the probabilities of all modules to be equal (uniform distribution), or

Assume the module probabilities to follow Zipf's law, specifying the ratio p_max/p_min, or

Assume the histogram of the module probabilities to behave like a bell curve, specifying the ratio p_max/p_min

Using the inputs, a report for sample size determination is created using the functions described above. The report contains the following sections:

Report section	Short description
Module probabilities	This section shows a plot with the probability of each module in the design space during library generation.
Expected minimum sample size	This part displays the expected minimum number of designs E[T] and the standard deviation.
Success probability	In this section, the report calculates the probability F(t) that the minimum number of designs T is smaller than or equal to a given sample size t. Moreover, a curve describing the success probability F(t) in function of an increasing sample size t is available, to determine a minimum sample size according to a probability cut-off.
Expected observed fraction of the total number of modules	Here, the fraction of the total number of modules in the design space that is expected to be observed is computed for a given sample size t. A saturation curve, displaying the expected fraction of modules observed in function of increasing sample size, is provided.
Number of occurrence of a specific module	In this last part, you can specify the probability p_j of a module of interest together with a particular sample size, to calculate a curve showing the probability for a module to occur k times (in function of k).

2. Case study Pluto notebook

The second Pluto notebook contains two case studies, illustrating the application of the BioCCP.jl package to real biological problems, more specifically:

(1) Studying the required sample size and related statistics for a genome-wide CRISPR experiment, based on a study from Chen et al. (2015) concerning tumour research in mouse models.

(2) Determining coverage of a combinatorial protein engineering experiment, based on a study from Duyvejonck et al. (2021) focusing on the development of endolysins as alternative antibiotics.

Getting started

Launch Pluto notebook from Browser

The Pluto notebooks can be launched directly from your browser using Binder (no installation of Julia/packages required):

Report-generating Pluto notebook:
Case study Pluto notebook: → To skip the run time and have immediate access to the results, the link provides an html file of the executed case study notebook.

Execute functions in Julia

(1) Install Julia

(2) Install BioCCP in the Julia REPL:

using Pkg; Pkg.add("BioCCP")

(3) Load the BioCCP package:

using BioCCP

Now you are ready for executing BioCCP functions in the Julia REPL.

Run the Pluto notebooks locally

Additionally, for using the Pluto notebooks, following steps need to be taken:

In the Julia REPL, hit the following command to install the Pluto package:

using Pkg; Pkg.add(name="Pluto", version="0.16.1")

Then start Pluto in the Julia REPL:

using Pluto; Pluto.run()

Finally, open the notebook file (report-generating notebook or case study notebook).

References

The implementation of formulas was based on the references below:

Doumas, A. V., & Papanicolaou, V. G. (2016). The coupon collector’s problem revisited: generalizing the double Dixie cup problem of Newman and Shepp. ESAIM: Probability and Statistics, 20, 367-399. doi: https://doi.org/10.1051/ps/2016016

Boneh, A., & Hofri, M. (1997). The coupon-collector problem revisited—a survey of engineering problems and computational methods. Stochastic Models, 13(1), 39-66. doi: https://doi.org/10.1080/15326349708807412

The case studies were based on the following references:

Chen, S., Sanjana, N. E., Zheng, K., Shalem, O., Lee, K., Shi, X., ... & Sharp, P. A. (2015). Genome-wide CRISPR screen in a mouse model of tumor growth and metastasis. Cell, 160(6), 1246-1260. doi: https://doi.org/10.1016/j.cell.2015.02.038Get

Duyvejonck, L., Gerstmans, H., Stock, M., Grimon, D., Lavigne, R., & Briers, Y. (2021). Rapid and High-Throughput Evaluation of Diverse Configurations of Engineered Lysins Using the VersaTile Technique. Antibiotics, 10(3), 293. doi: https://doi.org/10.3390/antibiotics10030293