Benchmark
Some preliminary experiments comparing the ChipSort performance with the Julia standard sort. Here we are not yet sorting a full array, but just trying to verify that the sorting and merge networks with SIMD pay off in the right conditions, sorting a small block of data of an appropriate size. Too little elements and there is too much overhead for the parallelism to be relevant. Too many elements and we start hitting the limits of the processor. When does our chip perform best?
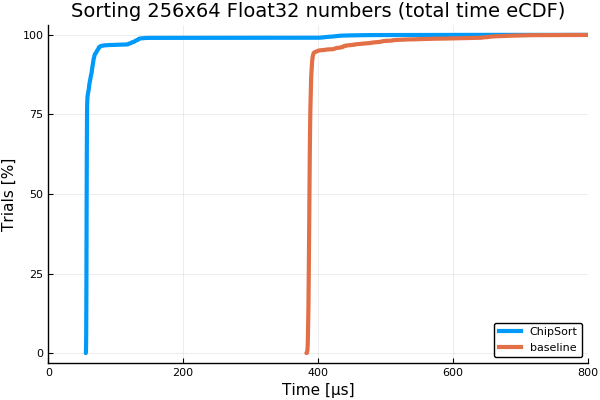
This graphic shows the time eCDF from times measured in 10,000 trials using BenchmarkTools.jl. The task is to sort 4 consecutive groups of 64 Float32 numbers in a 256 array. "Vector" means a SIMD.jl Vec array, that is supposed to e.g. sit inside a YMM AVX register.

Because this is such a small task there is a lot of variation in the measured times. The curve for ChipSort is quite more to the left, though, indicating we do get a speedup in this situation. It is not always the case, though.
In this next graphic we show the speed of ChipSort relative to the baseline. The task is different in each case, we are sorting the 256 values in groups of 8 times n, where n is the value in each column. As we can see, once we increase past 8x8 we lose the benefits from the techniques used in ChipSort.

By increasing the total size of the input array to 16k, although keeping the small size of the blocks we are sorting, the benchmark now results in less variation and also a larger speedup.
The same bar chart with different block sizes still shows that performance might degrade, but at the right situation the proposed technique can reach a relative speed of more than 6 times over the baseline.
