DiffusiveShockAccelerationModels.jl
This package provides a number of efficiency models for Diffuse Shock Acceleration (DSA). It provides a number of functions to calculate what fraction of the energy dissipated at a shock is used to accelerate Cosmic Rays (CRs). If you use this implementation in a publication please cite Böss et. al. (2023).
Install
As usual with Julia just run
] add DiffusiveShockAccelerationModelsMach number dendent efficiency models
Different authors found a number of models that describe the acceleration efficiency of CRs at shocks dependent on the sonic Mach number. Here we implemented the following DSA models:
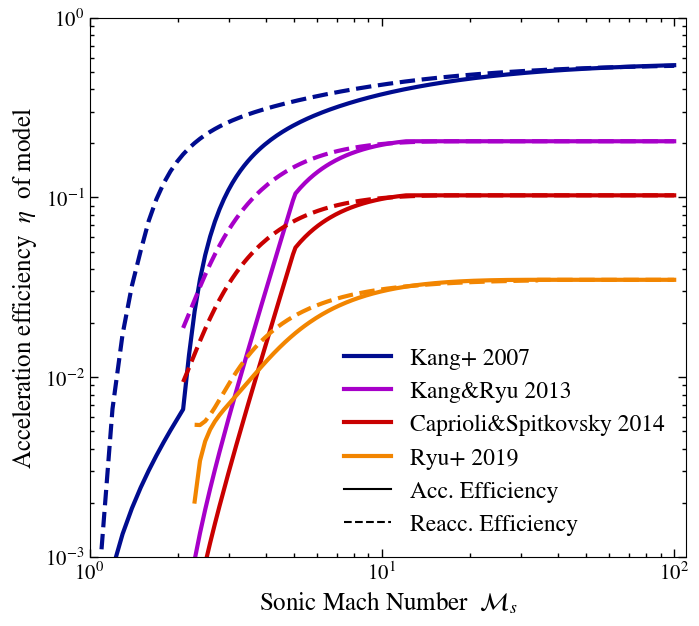
Missing docstring for Kang07. Check Documenter's build log for details.
Missing docstring for KR13. Check Documenter's build log for details.
Missing docstring for CS14. Check Documenter's build log for details.
Missing docstring for Ryu19. Check Documenter's build log for details.
Missing docstring for P16. Check Documenter's build log for details.
Magnetic field angle dependent efficiency models
Another parameter in the acceleration efficiency is the shock obliquity. Here we used the results from Pais et. al. (2019) who fit a functional form to the data by Caprioli&Spitkovsky (2014).
Missing docstring for η_B. Check Documenter's build log for details.
Ions
Ions are found to be accelerated primarily at quasi-parallel shocks. We provide two helper functions for this.
Missing docstring for ηB_acc_p. Check Documenter's build log for details.
Missing docstring for ηB_reacc_p. Check Documenter's build log for details.
Electrons
Electrons are found to be accelerated primarily at quasi-perpendicular shocks. We provide two helper functions for this.
Missing docstring for ηB_acc_e. Check Documenter's build log for details.
Missing docstring for ηB_reacc_e. Check Documenter's build log for details.
Usage
To use for example the mach number dependent model by Kang & Ryu (2013), combined with the shock obliquity model by Pais et. al. (2019)
using DiffusiveShockAccelerationModels
ηM_model = KR13() # Mach number dependent model
Mach = 5.0 # we assume a Mach 5 shock
θ_B = 0.1π # angle between shock normal and magnetic field vector
X_cr = 0.0 # X_cr = P_cr / P_th -> in this case no pre-existing CRs
# magnetic field angle dependent acc. efficiency
ηB = ηB_acc_p(θ_B)
# Mach number dependent acc. efficiency
ηM = η_Ms(ηM_model, Mach, X_cr)
# total efficiency
η_tot = ηB * ηM