Getting Started
Contents
Installation and usage
Installation:
] add DisjointCliqueCoverUsage:
using DisjointCliqueCoverInput data
We need first an undirected network of the SimpleGraph type as provided by package LightGraphs. For example, let us create the following small network:
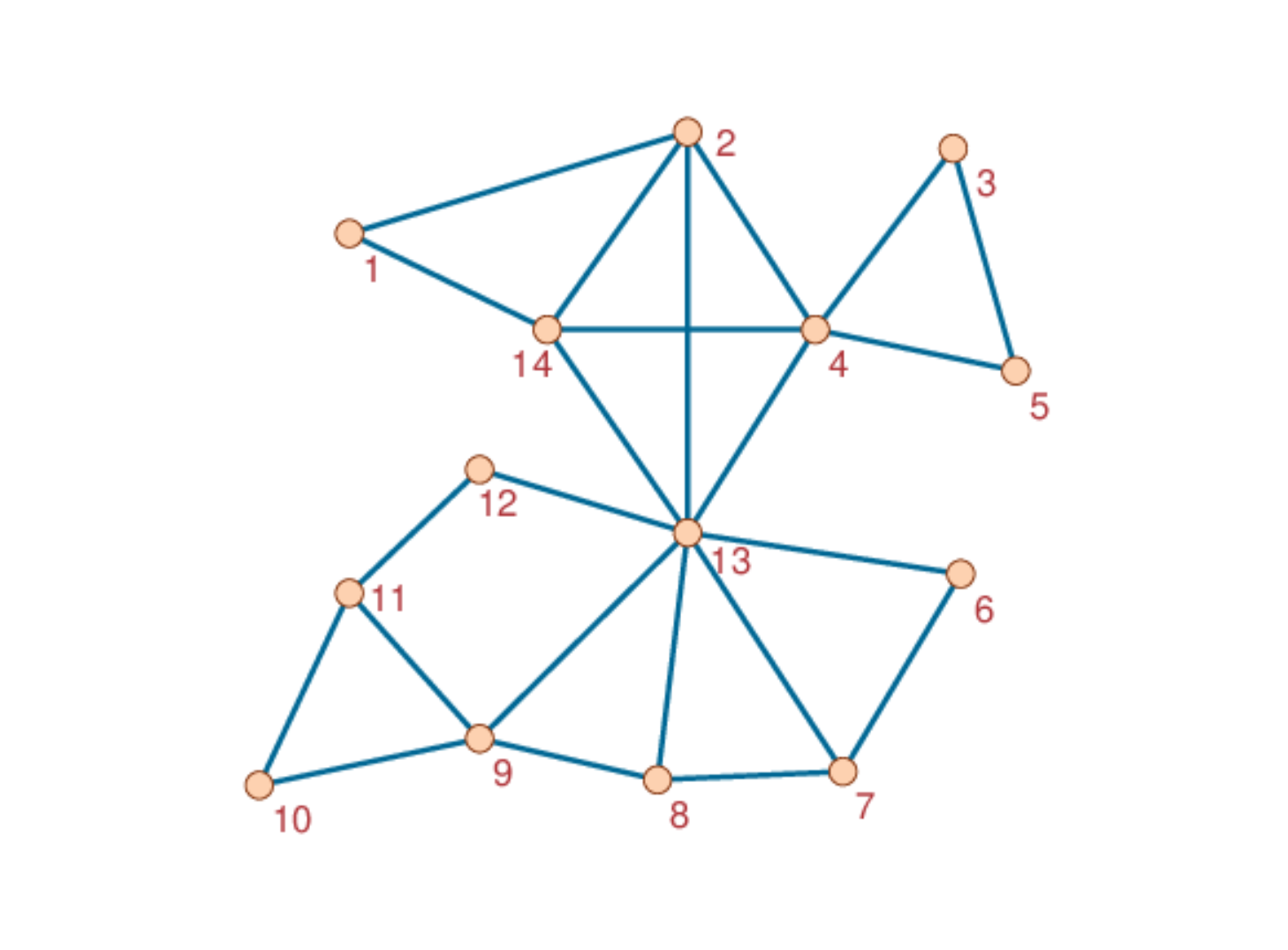
Using LightGraphs functions:
using LightGraphs
N = 14
edges_list = [(1, 2), (1, 14), (2, 4), (2, 13), (2, 14), (3, 4), (3, 5), (4, 5), (4, 13),
(4, 14), (6, 7), (6, 13), (7, 8), (7, 13), (8, 9), (8, 13), (9, 10), (9, 11),
(9, 13), (10, 11), (11, 12), (12, 13), (13, 14)]
G = SimpleGraph(N)
for e in edges_list
add_edge!(G, e[1], e[2])
endEdge-disjoint edge clique cover (EECC)
EECC requires to decide the maximum order of the cliques to consider:
m₀ = 4To estimate a minimal EECC, just call the get_EECC function:
eecc = get_EECC(G, m₀)The result is a list of the cliques that form the EECC, where each clique is indicated by the list of nodes it contains:
for c in eecc
println(c)
end[2, 4, 13, 14] [3, 4, 5] [6, 7, 13] [8, 9, 13] [9, 10, 11] [1, 2] [1, 14] [7, 8] [11, 12] [12, 13]
A graph can admit multiple minimal EECC, thus different executions may lead to different estimations. For example, for the same network but with maximum order m₀ = 3 we may get:
m₀ = 3
eecc = get_EECC(G, m₀)[1, 2, 14] [3, 4, 5] [4, 13, 14] [6, 7, 13] [8, 9, 13] [9, 10, 11] [2, 4] [2, 13] [7, 8] [11, 12] [12, 13]
but also
m₀ = 3
eecc = get_EECC(G, m₀)[1, 2, 14] [2, 4, 13] [3, 4, 5] [6, 7, 13] [8, 9, 13] [9, 10, 11] [4, 14] [7, 8] [11, 12] [12, 13] [13, 14]