Dispersal.jl
Dispersal.Dispersal — ModuleDispersal
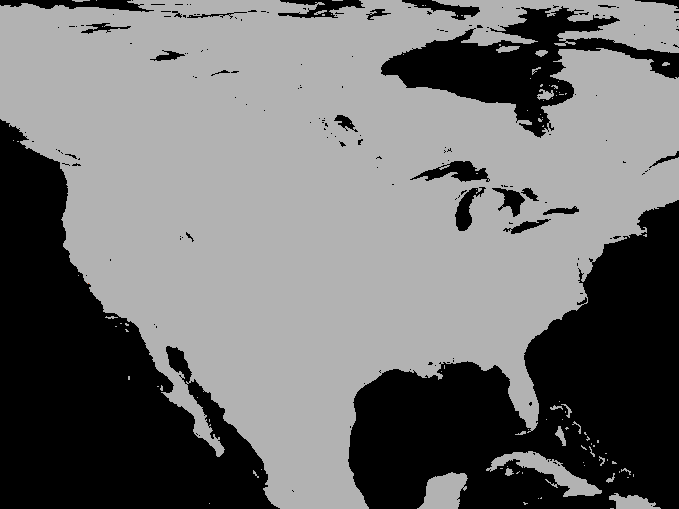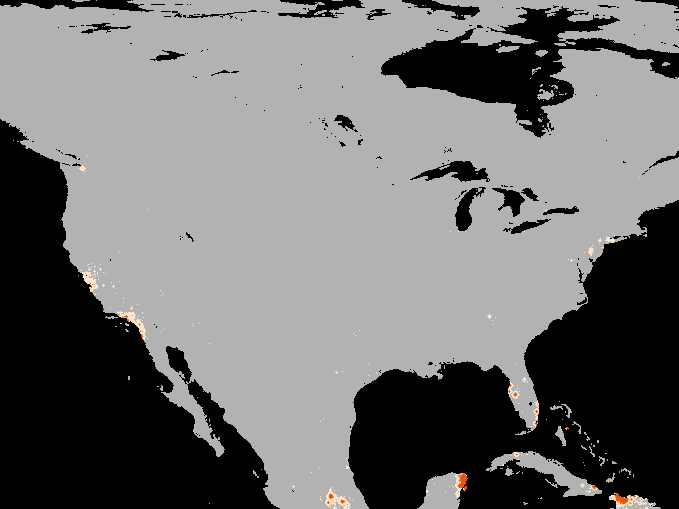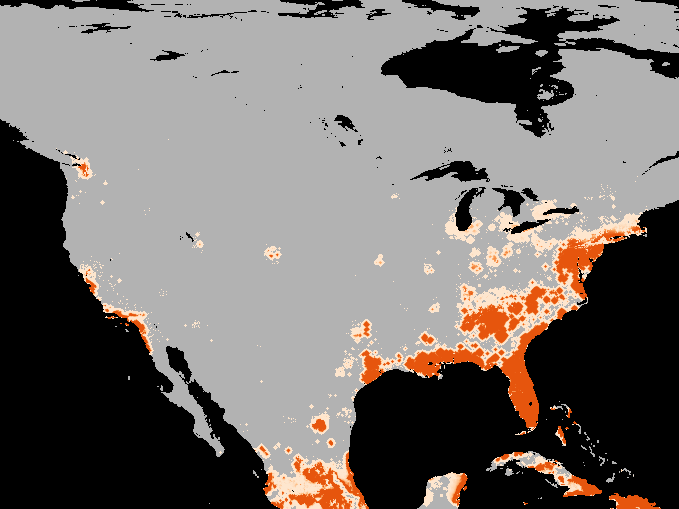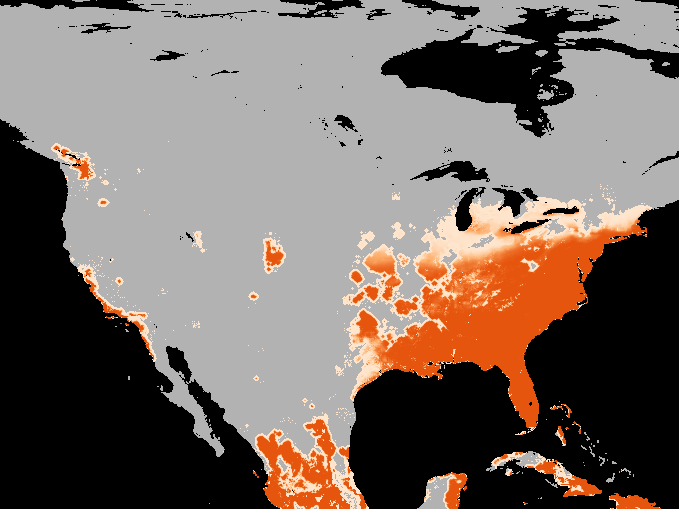
A simulation of the spotted-wing drosophola invasion of the continental United States as detailed in Maino, Schouten, and Umina (2021)
Dispersal.jl extends DynamicGrids.jl to provide model components and tools for grid-based simulations of organism dispersal.
Growth rates, dispersal kernels, Allee effects, and randomised jump and human assisted dispersal rules are provided. These components can be combined into complex dispersal models. Custom rules can easily added and combined with the provided set. See the documentation for examples and the lists of included rules.
DynamicGridsInteract provides an interactive interface for atom and jupyter notbooks (InteractOuput), desktop (ElectronOutput) and online web applications (ServerOuput), where complete models, including your custom rules, can be manipulated during live simulations.
DynamicGridsGtk provides GtkOutput for a simple graphical viewer.
GrowthMaps.jl can efficiently generate summarised raster data for vital rates (e.g. intrinsic growth rates) based on higher resolution and shorter interval environmental data.
Growth rules
Dispersal.GrowthRule — TypeGrowthRule <: CellRuleAbstract supertype for growth dynamics rules.
Dispersal.ExponentialGrowth — TypeExponentialGrowth <: CellRule
ExponentialGrowth(; rate, timestep, [nsteps_type])
ExponentialGrowth{R}(; rate, timestep, [nsteps_type])
ExponentialGrowth{R,W}(; rate, timestep, [nsteps_type])Exponential growth of population size N based on an intrinsic growth rate $r$, using the exact solution between timesteps $t$ and $t-1$:
\[N_t = N_{t-1}e^{r t}\]
Keywords
rate: Intrinsic growth rate. May be aNumber, anAuxarray or anotherGrid.timestep: Time step for the growth rate calculation, in a type compatible with the simulationtspan.nsteps_type: Specify the floating point type to use whennstepsis generated from the timestep, if it is required for type-stability or performance. The default isFloat64.
Pass grid Symbols to R or both R and W type parameters to use to specific grids.
Dispersal.LogisticGrowth — TypeLogisticGrowth <: GrowthRule
LogisticGrowth(; rate, carrycap, timestep, [nsteps_type])
LogisticGrowth{R}(; rate, carrycap, timestep, [nsteps_type])
LogisticGrowth{R,W}(; rate, carrycap, timestep, [nsteps_type])Logistic growth rate of population size $N$ based on an intrinsic growth rate $r$ and carry capacity $K$, using the exact solution between timesteps $t+1$ and $t$:
\[N_{t+1} = (N_t K) / (N_t + (K - N_t) e^{-rt})\]
Saturation only applies with positive growth.
Keywords
These may be a Number, an Aux array or another Grid:
rate: Intrinsic growth rate.carrycap: Carrying capacity.timestep: Time step for the growth rate, in a type compatible with the simulationtspan.nsteps_type: Specify the floating point type to use whennstepsis generated from the timestep, if it is required for type-stability or performance. The default isFloat64.
Pass grid Symbols to R or both R and W type parameters to use to specific grids.
Dispersal.ThresholdGrowth — TypeThresholdGrowth <: CellRule
ThresholdGrowth(; rate, threshold)
ThresholdGrowth{R}(; rate, threshold)
ThresholdGrowth{R,W}(; rate, threshold)Simple threshold mask. Values below a certain threshold are replaced with zero.
Keywords
These may be a Number, an Aux array or another Grid.
rate: Intrinsic growth rate.threshold: Minimum viability threshold below which population falls to zero.
Pass grid Symbols to R or both R and W type parameters to use to specific grids.
Mortality
Dispersal.Mortality — TypeMortality <: CellRuleAbstract super type for rules of survival effect For best performance these should be chained with other CellRule or following an NeighborhoodRule.
Dispersal.ExponentialMortality — TypeExponentialMortality <: Mortality
ExponentialMortality(; rate, threshold, timestep, [nsteps_type])
ExponentialMortality{R}(; rate, threshold, timestep, [nsteps_type])
ExponentialMortality{R,W}(; rate, threshold, timestep, [nsteps_type])Exponential mortality based on exposure threshold and mortality rate parameter, using exact solution.
Exponential mortality based on exposure grid $X$, an exposure threshold parameter $z$ and a mortality rate $r$ using exact solution between time $t$ and `$t+1$:
\[N_{t+1} = N_{t}e^{-r t(X-z)}\]
Keywords
rate: Mortality rate.threshold: Exposure threshold under which there is no effect.timestep: Time step for the growth rate, in a type compatible with the simulationtspan.nsteps_type: Specify the floating point type to use whennstepsis generated from the timestep, if it is required for type-stability or performance. The default isFloat64.
rate and threshold can be a Number, an Aux array or another Grid`.
Pass grid Symbols to R or both R and W type parameters to use to specific grids. R is a 2 Grids NamedTuple like Tuple{:population,:exposure} and W return only the first grid :population.
Dispersal.LoglogisticMortality — TypeLoglogisticMortality <: Mortality
LoglogisticMortality(; median, hillcoefficient, timestep, [nsteps_type])
LoglogisticMortality{R}(; median, hillcoefficient, timestep, [nsteps_type])
LoglogisticMortality{R,W}(; median, hillcoefficient, timestep, [nsteps_type])Loglogistic mortality based on median, $α$ and hill coefficient $β$.
Cumulative function of loglogistic:
\[F(x; α, β) = x^β/(α^β + x^β)\]
where $α>0$ is the scale and $β>0$ is the shape.
Keywords
median: Median of the loglogistic functionhillcoefficient: Hill's coefficient, a measure of ultrasensitivity (i.e. how steep is the response curve). May be aNumber, anAuxarray or anotherGrid.timestep: Time step for the mortality rate, in a type compatible with the simulationtspan.
Pass grid Symbols to R or both R and W type parameters to use to specific grids. R is a 2 Grids NamedTuple like Tuple{:population,:exposure} and W return only the first grid :population.
Allee effects
Dispersal.AlleeExtinction — TypeAlleeExtinction <: CellRule
AlleeExtinction(minfounders)
AlleeExtinction{R}(; minfounders=5.0)
AlleeExtinction{R,W}(minfounders)Causes extinction in a cell when a population is below a minimum number of individuals.
minfounders: minimum founding individuals required for a viable population. Must be a type that can be compared to the grid values usingisless.
Pass grid Symbols to R or both R and W type parameters to use to specific grids.
Local dispersal rules
Dispersal.InwardsDispersal — TypeInwardsPopulationDispersal <: NeighborhoodRule
InwardsPopulationDispersal(; kw...)
InwardsPopulationDispersal{R}(; kw...)
InwardsPopulationDispersal{R,W}(; kw...)Implements deterministic dispersal from populations in neighboring cells to the current cell.
The result should be identical to those obtained substituting InwardsDispersal for OutwardsDispersal but will perform better when populations are spread across the grid.
Keywords
neighborhood: Any DynamicGrids.jlNeighborhood, or an already constructedDispersalKernel. Using this keyword meansradiusis ignored, and for aDispersalKernel, all other keywords are ignored.neighborhood:Neighborhoodobject specifying the range from the origin of the discretised dispersal kernal. Defaults toWindow(radius).formulation: kernel formulation object holding the exact form of the kernal. DefaultExponentialKernel.cellsize: the cell size of the discretised kernal (i.e. simulation grid size). Default is 1.0.distancemethod:DistanceMethodobject for calculating distance between cells. The default isCentroidToCentroid.
Pass grid Symbols to R or both R and W type parameters to use to specific grids.
Dispersal.OutwardsDispersal — TypeOutwardsPopulationDispersal <: SetNeighborhoodRule
OutwardsPopulationDispersal(; kw...)
OutwardsPopulationDispersal{R}(; kw...)
OutwardsPopulationDispersal{R,W}(; kw...)Implements deterministic dispersal from the current cell to populations in neighboring cells.
This will make sense ecologically where cell populations are large, otherwise a randomised kernel may be more suitable.
The result should be identical to those obtained substituting OutwardsDispersal for InwardsDispersal but may be more efficient when a small number of cells are occupied. Conversely, it will become less efficient when a large proportion of the grid is occupied.
Keywords
neighborhood: Any DynamicGrids.jlNeighborhood, or an already constructedDispersalKernel. Using this keyword meansradiusis ignored, and for aDispersalKernel, all other keywords are ignored.neighborhood:Neighborhoodobject specifying the range from the origin of the discretised dispersal kernal. Defaults toWindow(radius).formulation: kernel formulation object holding the exact form of the kernal. DefaultExponentialKernel.cellsize: the cell size of the discretised kernal (i.e. simulation grid size). Default is 1.0.distancemethod:DistanceMethodobject for calculating distance between cells. The default isCentroidToCentroid.
Pass grid name Symbols to R and W type parameters to use specific grids.
Dispersal kernels
Kernels extend DynamicGrids.Neighborhood, and use neighbors() methods.
Dispersal.DispersalKernel — TypeDispersalKernel <: AbstractKernelNeighborhood
DispersalKernel(; kw...)Dispersal kernel for taking the dot product of the neighborhood and a matching kernel of weights. May hold any Neighborhood object: the kernel will be built to match the shape, using the folumation, cellsize and distancemethod.
Keyword Arguments
neighborhood: Any DynamicGrids.jlNeighborhood, or an already constructedDispersalKernel. Using this keyword meansradiusis ignored, and for aDispersalKernel, all other keywords are ignored.neighborhood:Neighborhoodobject specifying the range from the origin of the discretised dispersal kernal. Defaults toWindow(radius).formulation: kernel formulation object holding the exact form of the kernal. DefaultExponentialKernel.cellsize: the cell size of the discretised kernal (i.e. simulation grid size). Default is 1.0.distancemethod:DistanceMethodobject for calculating distance between cells. The default isCentroidToCentroid.
Dispersal.KernelFormulation — Typeabstract type KernelFormulationKernelFormulationAbstract supertype for functors that calculate the probability density based on distance.
Concrete implementations must define functor methods with the form:
(k::SomeKernel)(distance) = # do something with `distance` and `k`"Using an anonymous function would not allow rebuildable model parameters.
Dispersal.ExponentialKernel — TypeExponentialKernel <: KernelFormulation
ExponentialKernel(λ)Probability density function of distance $d$.
\[y = e^{-d/λ}\]
where λ is a shape parameter.
Dispersal.GeometricKernel — TypeGeometricKernel <: KernelFormulation
GeometricKernel(α)Probability density function of distance $d$.
The Geometric kernel has a power-law decrease.
\[y = (1+d)^α (α+1)(α+2) / (2 π)\]
where α is a shape parameter.
Dispersal.GaussianKernel — TypeGaussianKernel <: KernelFormulation
GaussianKernel(α)Probability density function of distance $d$.
\[y = 1/ (π α^2) e^{-d^2/α^2} \]
where α is a positive parameter.
Dispersal.WeibullKernel — TypeWeibullKernel <: KernelFormulation
WeibullKernel(α,β)Probability density function of distance $d$.
\[y =β /(2 π α^2) d^{β-2} e^{ -d^β/α^β} \]
where α and β are positive parameters.
Distance methods
Dispersal kernels can be calculated in a number of ways, giving different properties and dispersal rates due to interactions between the cell size and the dispersal distance.
Dispersal.DistanceMethod — Typeabstract type DistanceMethodDistanceMethodAbstract supertype for methods of calculating distances and discretised dispersal probabilities between cells in a grid. between cells in a grid.
Distance calculation methods include:
Which are adapted from: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"
The CentroidToArea method has not been implemented.
Dispersal.CentroidToCentroid — Typestruct CentroidToCentroid <: DistanceMethodCentroidToCentroid <: DistanceMethod
CentroidToCentroid()Calculates the discrete probability of dispersal between source and destination cell centroids. This is the naive method, but it will not handle low grid resolution well due to severe truncation.
See: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"
Dispersal.AreaToCentroid — TypeAreaToCentroid <: DistanceMethod
AreaToCentroid(subsampling)
AreaToCentroid(; subsampling=10.0)Calculates the discrete probability of dispersal between source cell area and destination centroid.
See: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"
Dispersal.AreaToArea — TypeAreaToArea <: DistanceMethod
AreaToArea(subsampling)
AreaToArea(; subsampling=10.0)Calculates the discrete probability of dispersal between source and destination based on cell areas.
See: "On the approximation of continuous dispersal kernels in discrete-space models, Joseph D. Chipperfield et al 2011"
Jump dispersal
Dispersal.JumpDispersal — TypeJumpDispersal <: SetCellRule
JumpDispersal(; prob_threshold, spotrange)
JumpDispersal{R}(; prob_threshold, spotrange)
JumpDispersal{R,W}(; prob_threshold, spotrange)Jump dispersal simulates a random long distance dispersal event, which occurs at a given probablity. A random cell within the spotrange is invaded by duplicating the entire population of the source cell at the destination cell.
Keyword Arguments
prob_threshold: probability of dispersal, between one and zero. May be aNumber, anAuxarray or anotherGrid:spotrange: number of cells in range of jumps, in any direction.
Pass grid Symbols to R or both R and W type parameters to use to specific grids.
Human driven dispersal
Dispersal.HumanDispersal — TypeHumanDispersal <: SetCellRule
HumanDispersal{R,W}(; kw...)Implements human-driven dispersal patterns using population density data.
The number of long-distance migrants from an origin is set proportional to the level of human population with the coefficient dispersalperpop. The destination of long-distance migration is is calculated by using the distance $d$ between and human population $H$ at origin cell $i$ and destination cell $j$ through a simple gravity function:
\[g_{i,j} = (H_i H_j)^β/(d_{i,j})^γ\]
where $β$ (human_exponent) and $γ$ (dist_exponent) are parameters. For each grid cell, a shortlist of size nshortlisted of the destination cells with the highest gravity are selected for use in the simulation.
The time taken for precalulation will depend on the scale argument. Values above 1 will downsample the grid to improve precalulation time and runtime performance. A high scale value is good for use in a live interface.
Keywords
mode: Dispersal mode: Defaults toBatchGroups(), otherwiseHeirarchicalGroups().human_pop: An array match the grid size containing human population data.cellsize: The size of the cell width, assuming they are squarescale: Downscaling factor to reduce memory use and improve performance, defaults to 4 which means a 1:16 ratio.aggregator: a function that aggregates cells, defualting tomean.human_exponent: human population exponent.dist_exponent: distance exponent.dispersalperpop: sets the number of dispersing individuals from the origin as a proportion of the level of human activity.max_dispersers: maximum number of dispersers in a single dispersal event.nshortlisted: length of the dispersal destination shortlist for each cell. Longer lists are more accurate in the tail of the distribution, but are slower to access.
Pass grid Symbols to R or both R and W type parameters to use to specific grids.
Dispersal.populate! — Functionpopulate!(A::AbstractMatrix, rule::HumanDispersal, [I...])
populate!(A::AbstractMatrix, cells::AbstractArray, [scale=1])Populate a matrix with the precalculated destinations from a HumanDispersal rule - either all of the or some subset if passed the I... indexing arguments. This is useful for plotting dispersal destinations, especially when used with GeoData.jl
Dispersal.populate — Functionpopulate(rule::HumanDispersal, [I...])Returns an array the size of human population matrix filled with all destination locataion, or with destinations specific to the passed-in indices I.
populate(cells::AbstractVector, size::Tuple, [scale::Int=1])Returns an array of size size populated from the vector of positions in cells rescaled by scale.

