Conway's Game of Life
using EasyABMStep 1: Create Agents and Model
We work with only patches in this model. The size of the grid in the model created is 20x20 and alive_percent is the fraction of patches that are alive initially.
model = create_2d_model(size = (20,20), alive_percent = 0.4)Step 2: Initialise the model
In the second step we initialise the patches by defining initialiser! function and sending it as an argument to init_model!. In the initialiser! function we randomly set patches to be either of color cl"green" or cl"white" (a named color, say "green", can be defined in EasyABM as cl"green" or as Col("green") or more generally as Col(0,1,0) or Col(0,1,0,1)). The patches with green color have their is_alive property set to true and the patches with white color have their is_alive property set to false. We specify the patch properties color and is_alive that we want to be recorded during time evolution in the props_to_record argument to the init_model! function.
function initialiser!(model)
for j in 1:model.size[2]
for i in 1:model.size[1]
if rand()<model.properties.alive_percent
model.patches[i,j].color = cl"green"
model.patches[i,j].is_alive = true
else
model.patches[i,j].color = cl"white"
model.patches[i,j].is_alive = false
end
end
end
end
init_model!(model, initialiser = initialiser!,
props_to_record=Dict("patches"=>Set([:color, :is_alive])))Step 3: Defining the step_rule! and running the model
In this step we implement the step logic of the Conway's Game of Life in the step_rule! function and run the model for 100 steps. Since Conway's model requires all patches to be updated at the same time, in the step_rule! function we first compute the is_alive property for all patches and then apply it to patches.
function calculate_vals(model)
vals = [false for i in 1:model.size[1], j in 1:model.size[2]]
for j in 1:model.size[2]
for i in 1:model.size[1]
patch = model.patches[i,j]
nbrs = neighbor_patches_moore((i,j), model, 1)
num_alive = 0
for nbr in nbrs
num_alive+= model.patches[nbr...].is_alive
end
condition1 = patch.is_alive && ((num_alive == 2) || (num_alive == 3))
condition2 = !(patch.is_alive) && (num_alive == 3)
if condition1 || condition2
vals[i,j] = true
end
end
end
return vals
end
function apply_vals!(model, vals)
for j in 1:model.size[2]
for i in 1:model.size[1]
is_alive = vals[i,j]
model.patches[i,j].is_alive = is_alive
model.patches[i,j].color = is_alive ? cl"green" : cl"white"
end
end
end
function step_rule!(model)
vals = calculate_vals(model)
apply_vals!(model, vals)
end
run_model!(model, steps=100, step_rule = step_rule! )In order to draw the model at a specific frame, say 4th, one can use draw_frame(model, frame = 4, show_patches=true). If one wants to see the animation of the model run, it can be done as
animate_sim(model, show_patches=true)
After defining the step_rule! function we can also choose to create an interactive application (which currently works in Jupyter with WebIO installation) as shown below. It is recommended to define a fresh model and not initialise it with init_model! or run with run_model! before creating interactive app.
model = create_2d_model(size = (20,20), alive_percent = 0.4)
create_interactive_app(model, initialiser= initialiser!,
props_to_record=Dict("patches"=>Set([:color, :is_alive])),
step_rule= step_rule!,
model_controls=[
(:alive_percent, "slider", 0:0.01:1.0)
],
frames=200, show_patches=true) 
Step 4: Fetch Data
We can fetch the data of number alive patches as follows.
df = get_nums_patches(model, patch-> patch.is_alive, labels=["Alive"],
plot_result = true)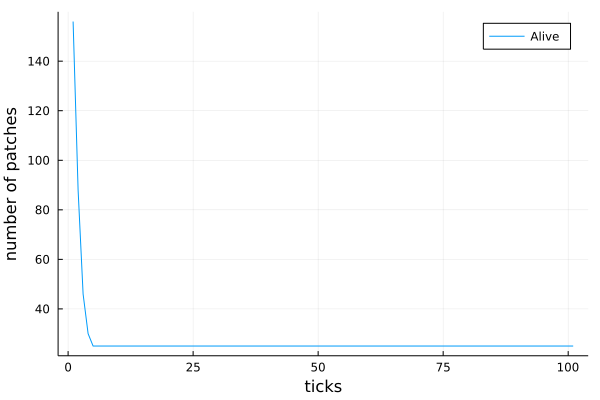
References
- https://en.wikipedia.org/wiki/Conway%27sGameof_Life