Fock diagram of free electrons
Tags: #many-electron-problem, #UEG, #feynman-diagram
0.1.1 Bare electron & Yukawa/Coulomb interaction
- The bare electron dispersion $\epsilon_k=k^2/2m$
- Independent of spin factor.
0.1.1.1 3D Electron Gas
- Interaction:
\[v(r)=\frac{e^2 \exp(-\lambda r)}{r}\rightarrow v_q=\frac{4\pi e^2}{q^2+\lambda^2}\]
\[\Sigma_x(k) = -\int \frac{d^3q}{(2\pi)^3} n_q v_{k-q}=-\int_0^{\infty} \frac{ 2\pi n_q q^2 dq}{8\pi^3}\int_{-1}^1 dx \frac{4\pi e^2}{(k^2+q^2+2 k q x)+\lambda^2}\]
\[=-\frac{e^2}{\pi}\int_0^{\infty} n_q q^2 dq\int_{-1}^1\frac{dx}{k^2+q^2+\lambda^2+2 k q\,x}\]
- At $T=0$, integrate $x$ first, we obtain
\[\Sigma_x(k)=\frac{e^2}{2\pi\,k}\int_0^{\infty} dq n_q q \ln\left(\frac{\lambda^2+(k-q)^2}{\lambda^2+(k+q)^2}\right)\]
- Next we introduce new variables $x=k/\lambda$ and $y=q/\lambda$ and $x_F=k_F/\lambda$ to obtain
\[\Sigma_x(k=\lambda x)=-\frac{\lambda e^2}{2\pi x}\int_0^{x_F} dy y \ln\left(\frac{1+(x+y)^2}{1+(x-y)^2}\right)\]
\[=-\frac{\lambda e^2}{2\pi} \left[ 2 x_F + 2\arctan(x-x_F)-2\arctan(x+x_F)-\frac{1-x^2+x_F^2}{2 x}\ln\left(\frac{1+(x-x_F)^2}{1+(x+x_F)^2}\right) \right]\]
- We conclude
\[ \Sigma_x(k)=-\frac{e^2 k_F}{\pi} \left[ 1 + \frac{\lambda}{k_F} \arctan(\frac{k-k_F}{\lambda})-\frac{\lambda}{k_F} \arctan(\frac{k+k_F}{\lambda}) -\frac{(\lambda^2-k^2+k_F^2)}{4 k\, k_F} \ln\left(\frac{\lambda^2+(k-k_F)^2}{\lambda^2+(k+k_F)^2}\right) \right]\]
- For Coulomb interaction $\lambda=0$,
\[\Sigma_x(k)=-\frac{e^2 k_F}{\pi} \left[ 1 +\frac{(k^2-k_F^2)}{2 k\, k_F} \ln\left|\frac{k-k_F}{k+k_F}\right| \right]\]
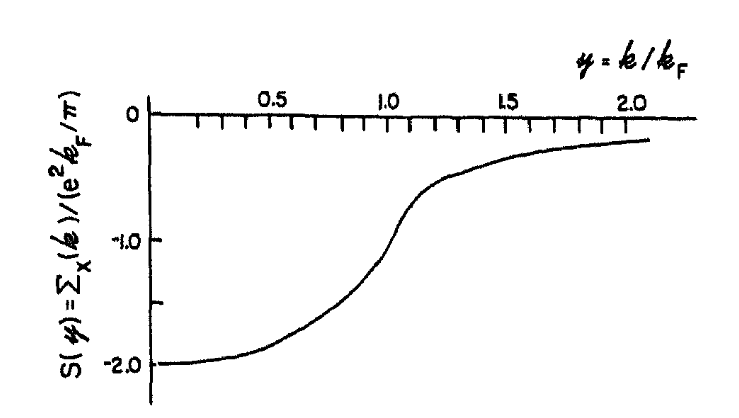
The effective mass diverges at the Fermi surface:
\[ \frac{m}{m^*}=1+m\frac{\partial^2 \Sigma_x (k)}{\partial k^2}=1-\frac{e^2 m}{2\pi k^2}\left[2+\frac{k^2+k_F^2}{k}\ln\left|\frac{k-k_F}{k+k_F}\right|\right]\]
0.1.1.2 2D Electron Gas
- Interaction (2D Yukawa interaction):
\[v_q=\frac{4\pi e^2}{q^2+\lambda^2}\]
- The Fock diagram,
\[\Sigma_x(k) = -\int \frac{d^2q}{(2\pi)^2} n_q v_{k-q}=-\int_0^{\infty}\frac{ n_q q dq}{4\pi^2}\int_{0}^{2\pi} d\theta \frac{4\pi e^2 }{(k^2+q^2+2 k q \cos \theta)+\lambda^2}\]
\[=-\frac{e^2}{\pi}\int_0^{\infty} n_q q dq \int_{0}^{2\pi}\frac{d\theta}{k^2+q^2+\lambda^2+2 k q\,\cos \theta}\]
- At $T=0$, use the integral $\int_0^{2\pi} \frac{d\theta}{a+\cos\theta}=\frac{2\pi}{\sqrt{a^2-1}}$ for $a>1$,
\[\Sigma_x(k)=-e^2\int_0^{k_F} \frac{dq^2}{\sqrt{(k^2+q^2+\lambda^2)^2-4 k^2 q^2}}=-e^2\int_{\lambda^2-k^2}^{k_F^2+\lambda^2-k^2} \frac{dx}{\sqrt{x^2+4 k^2 q^2}}\]
Use the integral $\int \frac{dx}{\sqrt{x^2+1}}=\ln (\sqrt{x^2+1}+x)+\text{Const}=\text{arcsinh}(x)+\text{Const}$
For Yukawa interaction $\lambda>0$,
\[\Sigma_x(k)=-e^2 \ln \frac{\sqrt{(k_F^2+\lambda^2-k^2)^2+4k^2\lambda^2}+k_F^2+\lambda^2-k^2}{\sqrt{(\lambda^2-k^2)^2+4k^2\lambda^2}+\lambda^2-k^2}\]
- Or equivalently,
\[\Sigma_x(k)=-e^2 \ln \frac{\sqrt{(k_F^2+\lambda^2-k^2)^2+4k^2\lambda^2}+k_F^2+\lambda^2-k^2}{2\lambda^2}\]
For the Coulomb interaction $\lambda=0$, the integral diverges. The problem is not well-defined.
- Interaction (3D Yukawa interaction in the plane):
\[v(r)=\frac{e^2 \exp(-\lambda r)}{r}\rightarrow v_q=\frac{2\pi e^2}{\sqrt{q^2+\lambda^2}}\]
- The Fock diagram,
\[\begin{aligned} \Sigma_x(k) = -\int \frac{d^2q}{(2\pi)^2} n_q v_{k-q} &=-\int_0^{\infty}\frac{ n_q q dq}{4\pi^2}\int_{0}^{2\pi} d\theta \frac{2\pi e^2 }{\sqrt{k^2+q^2+2 k q \cos \theta+\lambda^2}} \\ &=-\frac{e^2}{2\pi k}\int_0^{\infty} n_q dq \left[\sqrt{(k+q)^2+\lambda^2} - \sqrt{(k-q)^2+\lambda^2} \right] . \end{aligned}\]
- At $T=0$,
\[\begin{aligned} \Sigma_x(k) &= -\frac{e^2}{2\pi k}\int_0^{k_F} dq \left[\sqrt{(k+q)^2+\lambda^2} - \sqrt{(k-q)^2+\lambda^2} \right] \\ &=-\frac{e^2}{4\pi k} \left\{(k-k_F)\sqrt{(k-k_F)^2+\lambda^2}+ (k+k_F)\sqrt{(k+k_F)^2+\lambda^2} -2k\sqrt{k^2+\lambda^2} +\lambda^2 \ln \frac{\left[k-k_F+\sqrt{(k-k_F)^2+\lambda^2}\right] \left[k+k_F+\sqrt{(k+k_F)^2+\lambda^2}\right]}{ (k+\sqrt{k^2+\lambda^2})^2} \right\} . \end{aligned}\]
- For Coulomb interaction $\lambda=0$,
\[\Sigma_x(k)= -\frac{e^2}{4\pi k} \left[(k-k_F)|k-k_F| +(k+k_F)|k+k_F| - 2k|k| \right] .\]
- For $k\to 0$
\[\Sigma_x(k=0)= -\frac{e^2}{\pi} \left(\sqrt{k_F^2+\lambda^2}-\lambda \right) .\]
Reference:
- GW for electron gas
- Mahan, Gerald D. Many-particle physics. Springer Science & Business Media, 2013. Chapter 5.1