EquilibratedFlux.jl
This package is based on Gridap.jl to provide post-processing tools to calculate reconstructed fluxes associated to the given approximate solution of a PDE.
For simplicity, we consider here the Poisson equation
\begin{align}
- \Delta u &= f &&\text{in }\Omega\\
u &= g &&\text{on }\partial\Omega.
\end{align}
We suppose we have already computed a conforming approximation $u_h \in V_h\subset H^1_0(\Omega)$ to the solution $u$ in Gridap.jl by solving
(\nabla u_h, \nabla v_h) = (f, v_h)\quad\forall v_h\in V_h,
The EquilibratedFlux.jl library then provides the tools to compute a reconstructed flux
associated to $u_h$. This flux, obtained by postprocessing, is an approximation to the numerical flux, i.e.
\sigma_h \approx -\nabla u_h.
This flux has the important property of being "conservative over faces" in the sense that
\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).
We provide two functions to obtain such an object:
build_equilibrated_flux
and
build_averaged_flux
both provide reconstructed fluxes, which we denote by $\sigma_{\mathrm{eq},h}$
and $\sigma_{\mathrm{ave},h}$ respectively.
In addition to the properties listed above, the equilibrated flux $\sigma_{\mathrm{eq},h}$ satisfies the so-called equilibrium condition, i.e., for piecewise polynomial $f$, we have
\nabla\cdot\sigma_{\mathrm{eq},h} = f.
More details can be found in the documentation.
Examples / Tutorials
Error estimation
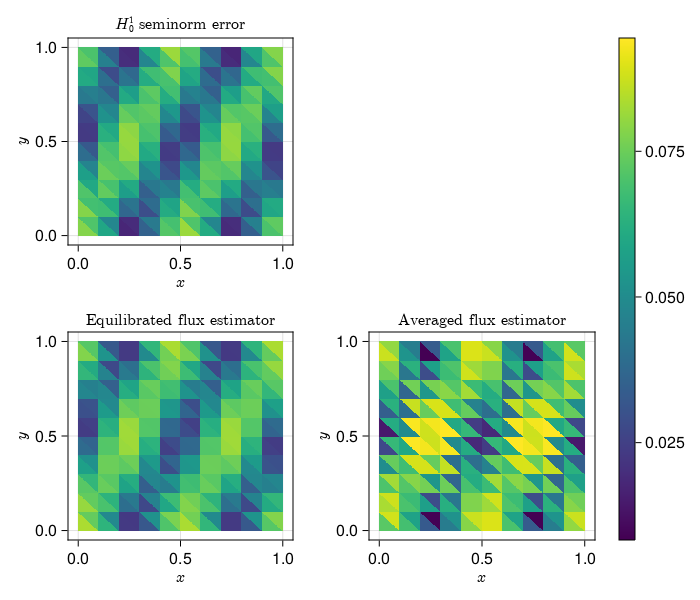
The reconstructed flux is the main ingredient in computing a posteriori error estimators.
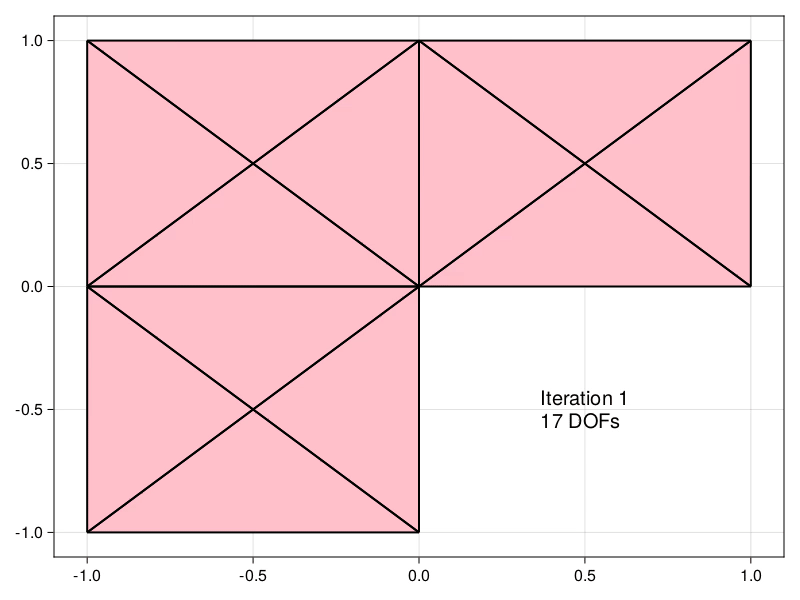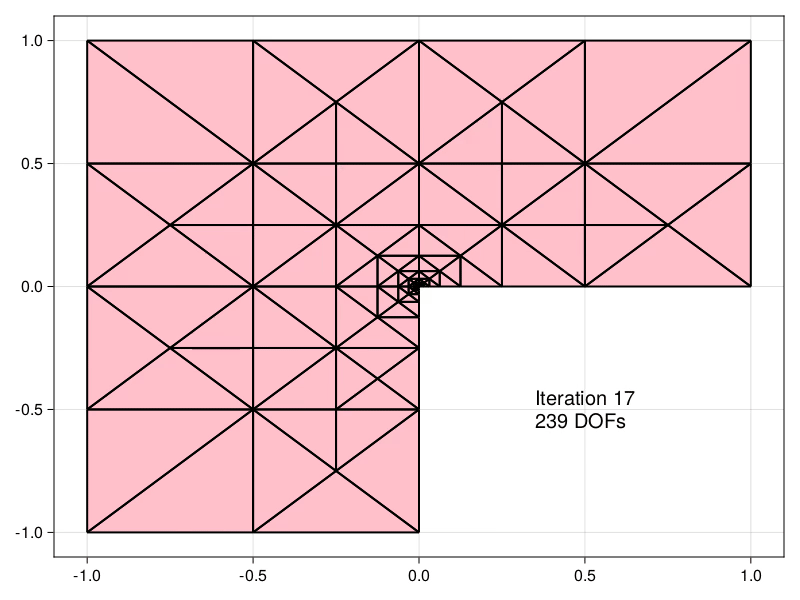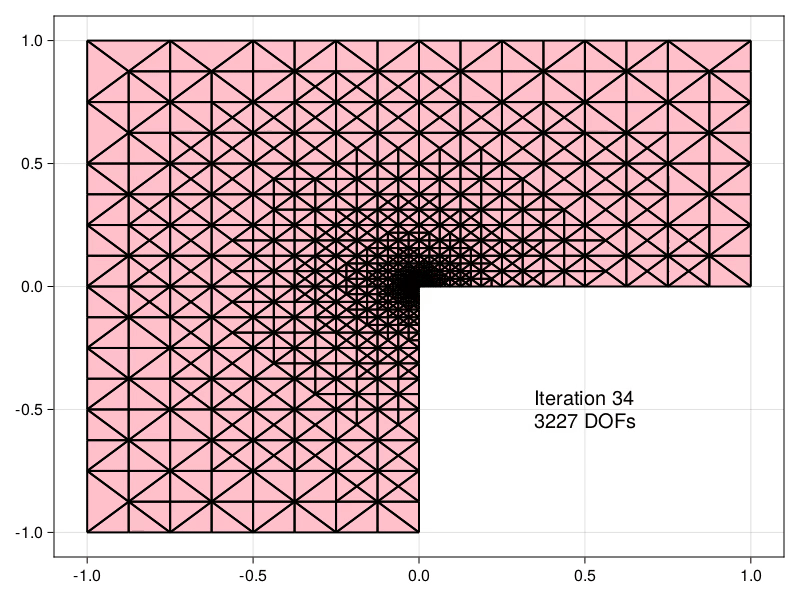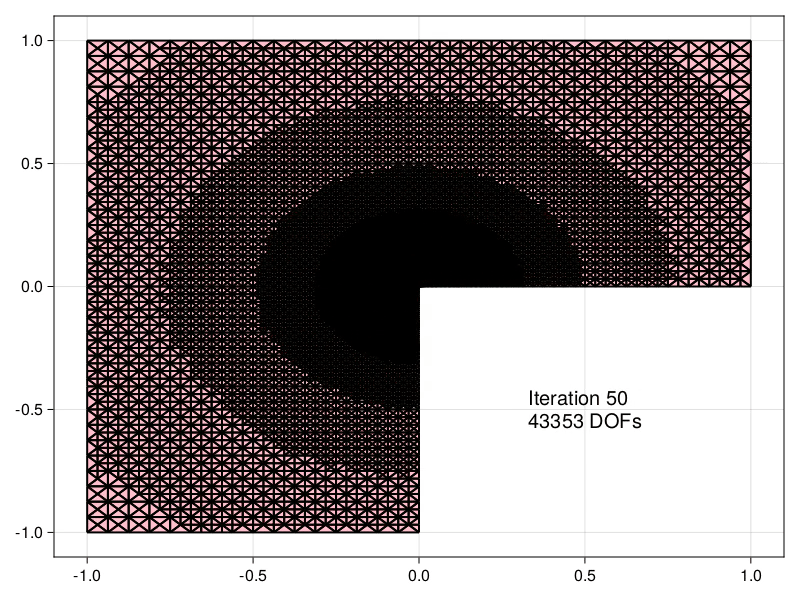
Mesh refinement
Estimators obtained using the equilibrated flux can be used to drive an Adaptive Mesh Refinement (AMR) precedure, demonstrated here for the Laplace problem in an L-shaped domain.