FinanceModels.jl
FinanceModels.jl provides a set of composable contracts, models, and functions that allow for modeling of both simple and complex financial instruments. The resulting models, such as discount rates or term structures, can then be used across the JuliaActuary ecosystem to perform actuarial and financial analysis.
Additionally, the models can be used to project contracts through time: most basically as a series of cashflows but more complex output can be defined for contracts.
QuickStart
using FinanceModels
# a set of market-observed prices we wish to calibrate the model to
# annual effective unless otherwise specified
q_rate = ZCBYield([0.01,0.02,0.03]);
q_spread = ZCBYield([0.01,0.01,0.01]);
# bootstrap a linear spline yield model
model_rate = fit(Spline.Linear(),q_rate,Fit.Bootstrap());⠀
model_spread = fit(Spline.Linear(),q_spread,Fit.Bootstrap());
# the zero rate is the combination of the two underlying rates
zero(m_spread + m_rate,1) # 0.02 annual effective rate
# the discount is the same as if we added the underlying zero rates
discount(m_spread + m_rate,0,3) ≈ discount(0.01 + 0.03,3) # true
# compute the present value of a contract (a cashflow of 10 at time 3)
present_value(m_rate,Cashflow(10,3)) # 9.15...Overview of FinanceModels
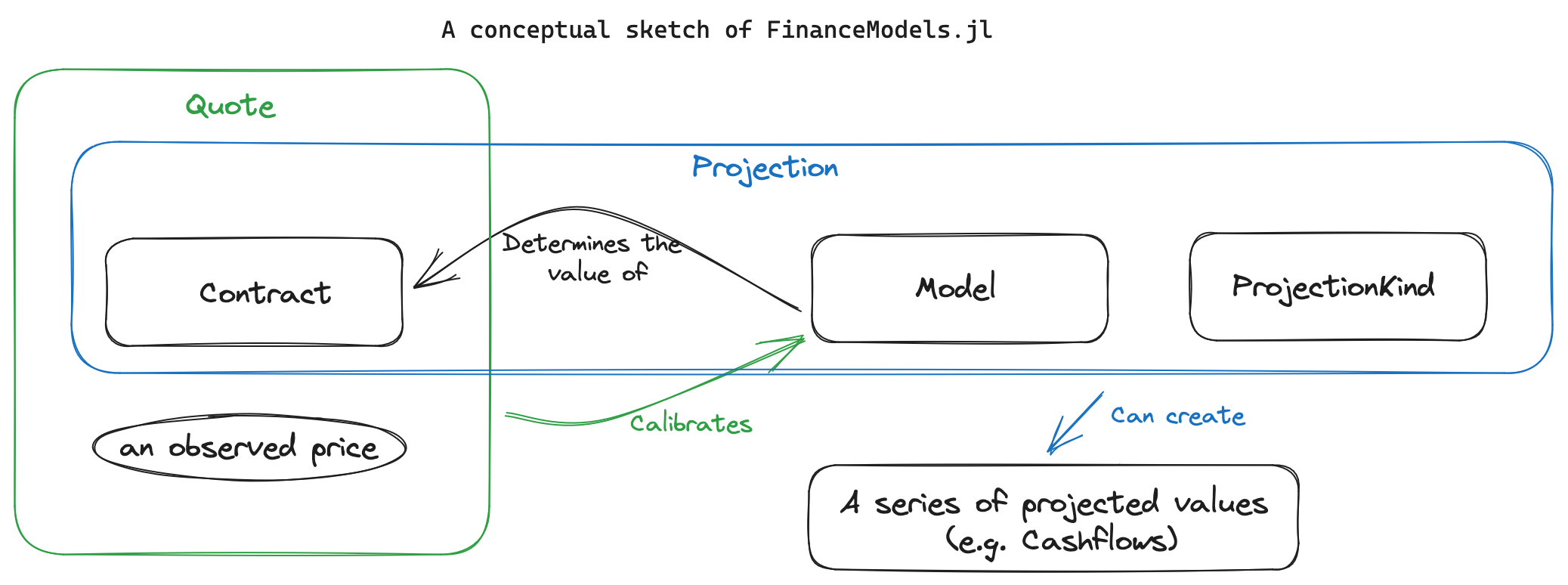
Often we start with observed or assumed values for existing contracts. We want to then use those assumed values to extend the valuation logic to new contracts. For example, we may have a set of bond yields which we then want to discount a series of insurance obligations.
In the language of FinanceModels, we would have a set of Quotes which are used to fit a Model. That model is then used to discount a new series of cashflows.
That's just an example, and we can use the various components in different ways depending on the objective of the analysis.
Contracts and Quotes
Contracts are a way to represent financial obligations. These can be valued using a model, projected into a future steam of values, or combined with assumed prices as a Quote.
Included are a number of primitives and convenience methods for contracts:
Existing structs:
CashflowBond.FixedBond.FloatingForward(an obligation with a forward start time)Composite(combine two other contracts, e.g. into a swap)EuroCallCommonEquity
Commonly, we deal with conventions that imply a contract and an observed price. For example, we may talk about a treasury yield of 0.03. This is a description that implies a Quoteed price for an underling fixed bond. In FinanceModels, we could use CMTYield(rate,tenor) which would create a Quote(price,Bond.Fixed(...)). In this way, we can conveniently create a number of Quotes which can be used to fit models. Such convenience methods include:
ZCBYieldZCBPriceCMTYieldParYieldParSwapYieldForwardYield
FinanceModels offers a way to define new contracts as well.
Cashflows
A Cashflows obligation are themselves a contract, but other contracts can be considered as essentially anything that can be combined with assumptions (a model) to derive a collection of cashflows.
For example, a obligation that pays 1.75 at time 2 could be represented as: Cashflow(1.75,2).
Models
Models are objects that can be fit to observed prices and then subsequently used to make valuations of other cashflows/contracts.
Yield models include:
Yield.Constant- Bootstrapped
Splines Yield.SmithWilsonYield.NelsonSiegelYield.NelsonSiegelSvensson
Yield-related functions
The models can be used to compute various rates of interest:
discount(curve,from,to)ordiscount(curve,to)gives the discount factoraccumulation(curve,from,to)oraccumulation(curve,to)gives the accumulation factorzero(curve,time)orzero(curve,time,Frequency)gives the zero-coupon spot rate for the given time.forward(curve,from,to)gives the zero rate between the two given timespar(curve,time;frequency=2)gives the coupon-paying par equivalent rate for the given time.
Other models include:
BlackScholesMertonderivative valuation
Plotting of Yield Curves
In interactive sessions (e.g. REPL, Notebooks, VS Code, etc.) you can get a pretty printing of yield curves by also using UnicodePlots.jl, for example:
julia> using FinanceModels
julia> q_rate = ZCBYield.([0.01, 0.02, 0.03,0.04,0.03],[1,3,5,10,20]);
julia> fit(Spline.PolynomialSpline(3), q_rate, Fit.Bootstrap())
FinanceModels.Yield.Spline{DataInterpolations.CubicSpline{Vector{Float64}, Vector{Float64}, Vector{Float64}, Vector{Float64}, true, Float64}}([0.009950330853168092, 0.009950330853168092, 0.019802627296179747, 0.02955880224154443, 0.0, 1.0, 2.0, 3.0])
julia> using UnicodePlots
julia> fit(Spline.PolynomialSpline(3), q_rate, Fit.Bootstrap()) # after importing UnicodePlots
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Yield Curve (FinanceModels.Yield.Spline)⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
┌────────────────────────────────────────────────────────────┐
0.04 │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠤⠖⠒⠊⠉⠉⠉⠒⠒⠢⠤⣄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│ Zero rates
│⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠔⠋⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠑⠒⢄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⠖⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠑⠢⣄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡔⠁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⠒⢄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⠀⠀⠀⠀⠀⢠⠎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⠓⠤⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⠀⠀⠀⠀⢠⠎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠑⠦⣄⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⠀⠀⠀⢠⠇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠉⠓⠦⣄⡀⠀⠀⠀⠀⠀⠀⠀⠀│
Continuous │⠀⠀⠀⠀⠀⢠⠇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠈⠉⠒⠒⠦⠤⠤⠤⠤│
│⠀⠀⠀⠀⢀⠎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⢀⡎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⢀⠎⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠒⠒⠃⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
│⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
0 │⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀│
└────────────────────────────────────────────────────────────┘
⠀0⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀time⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀30⠀
[!NOTE] This was built-in prior to v4.9 of FinanceModels. It has been split out to materially speed up
using FinanceModels.
Projections
Most basically, we can project a contract into a series of Cashflows:
julia> b = Bond.Fixed(0.04,Periodic(2),3)
FinanceModels.Bond.Fixed{Periodic, Float64, Int64}(0.04, Periodic(2), 3)
julia> collect(b)
6-element Vector{Cashflow{Float64, Float64}}:
Cashflow{Float64, Float64}(0.02, 0.5)
Cashflow{Float64, Float64}(0.02, 1.0)
Cashflow{Float64, Float64}(0.02, 1.5)
Cashflow{Float64, Float64}(0.02, 2.0)
Cashflow{Float64, Float64}(0.02, 2.5)
Cashflow{Float64, Float64}(1.02, 3.0)However, Projections allow one to combine three elements which can be extended to define any desired output (such as amortization schedules, financial statement projections, or account value rollforwards). The three elements are:
- the underlying contract of interest
- the model which includes assumptions of how the contract will behave
- a
ProjectionKindwhich indicates the kind of output desired (cashflow stream, amortization schedule, etc...)
Examples
A fixed bond that needs no valuation model (NullModel()) to define its projected gross cashflows:
Projection(Bond.Fixed(0.04,Periodic(2),3),NullModel(),CashflowProjection())Plotting Projections
A CashflowProjection or a vector of Cashflows can be plotted with the Makie family of plotting packages.
using FinanceModels, CairoMakie
proj = Projection(Bond.Fixed(0.10,Periodic(2),20),NullModel(),CashflowProjection())
# a stem plot:
stem(proj)Will produce:
Fitting Models
Fitting Models
Model Method
| |
|------------| |---------------|
fit(Spline.Cubic(), CMTYield.([0.04,0.05,0.055,0.06,0055],[1,2,3,4,5]), Fit.Bootstrap())
|-------------------------------------------------|
|
Quotes- Model could be
Spline.Linear(),Yield.NelsonSiegelSvensson(),Equity.BlackScholesMerton(...), etc. - Quote could be
CMTYields,ParYields,Option.Eurocall, etc. - Method could be
Fit.Loss(x->x^2),Fit.Loss(x->abs(x)),Fit.Bootstrap(), etc.
This unified way to fit models offers a much simpler way to extend functionality to new models or contract types.
Using Models
After being fit, models can be used to value contracts:
present_value(model,cashflows)Additionally, ActuaryUtilities.jl offers a number of other methods that can be used, such as duration, convexity, price which can be used for analysis with the fitted models.
Rates
Rates are types that wrap scalar values to provide information about how to determine discount and accumulation factors.
There are two Frequency types:
Periodic(m)for rates that compoundmtimes per period (e.g.mtimes per year if working with annual rates).Continuous()for continuously compounding rates.
Examples
Continuous(0.05) # 5% continuously compounded
Periodic(0.05,2) # 5% compounded twice per periodThese are both subtypes of the parent Rate type and are instantiated as:
Rate(0.05,Continuous()) # 5% continuously compounded
Rate(0.05,Periodic(2)) # 5% compounded twice per periodRates can also be constructed by specifying the Frequency and then passing a scalar rate:
Periodic(1)(0.05)
Continuous()(0.05)Conversion
Convert rates between different types with convert. E.g.:
r = Rate(FinanceModels.Periodic(12),0.01) # rate that compounds 12 times per rate period (ie monthly)
convert(FinanceModels.Periodic(1),r) # convert monthly rate to annual effective
convert(FinanceModels.Continuous(),r) # convert monthly rate to continuousArithmetic
Adding, substracting, multiplying, dividing, and comparing rates is supported.
Guide and Documentation
A guide which explains more about the components of the package and from-scratch examples of extending the package is available in the documenation
Exported vs Un-exported Functions
Generally, CamelCase methods which construct a datatype are exported as they are unlikely to conflict with other parts of code that may be written. For example, rate is un-exported (it must be called with FinanceModels.rate(...)) because rate is likely a very commonly defined variable within actuarial and financial contexts and there is a high risk of conflicting with defined variables.
Consider using import FinanceModels which would require qualifying all methods, but alleviates any namespace conflicts and has the benefit of being explicit about the calls (internally we prefer this in the package design to keep dependencies and their usage clear).
Internals
For time-variant FinanceModels (ie yield curves), the inputs are converted to spot rates and interpolated using quadratic B-splines by default (see documentation for alternatives, such as linear interpolations).
Combination Implementation
Combinations track two different curve objects and are not combined into a single underlying data structure. This means that you may achieve better performance if you combine the rates before constructing a FinanceModels representation. The exception to this is Constant curves, which do get combined into a single structure that is as performant as pre-combined rate structure.
Related Packages
InterestRates.jlspecializes in fast rate calculations aimed at valuing fixed income contracts, with business-day-level accuracy.- Comparative comments:
FinanceModels.jldoes not try to provide as precise controls over the timing, structure, and interpolation of the curve. Instead,FinanceModels.jlprovides a minimal, but flexible and intuitive interface for common modeling needs.
- Comparative comments:

