Forest fire
The forest fire model is defined as a cellular automaton on a grid. A position can be empty or occupied by a tree which is ok, burning or burnt. We implement a slightly different ruleset to that of Drossel and Schwabl (1992), so that our implementation can be compared with other ABM frameworks
- A burning position turns into a burnt position
- A tree will burn if at least one neighbor is burning
The forest has an innate density, which is the proportion of trees initialized as green, however all trees that reside on the left side of the grid are burning. The model is also available from the Models module as Models.forest_fire.
Defining the core structures
Cellular automata don't necessarily require an agent-like structure. Here we will demonstrate how a model focused solution is possible.
using Agents, Random
using CairoMakie
@agent struct Automata(GridAgent{2}) endThe agent type Automata is effectively a dummy agent, for which we will invoke dummystep when stepping the model.
We then make a setup function that initializes the model.
function forest_fire(; density = 0.7, griddims = (100, 100), seed = 2)
space = GridSpaceSingle(griddims; periodic = false, metric = :manhattan)
rng = Random.MersenneTwister(seed)
# The `trees` field is coded such that
# Empty = 0, Green = 1, Burning = 2, Burnt = 3
forest = StandardABM(Automata, space; rng, model_step! = tree_step!,
properties = (trees = zeros(Int, griddims),), container = Vector)
for I in CartesianIndices(forest.trees)
if rand(abmrng(forest)) < density
# Set the trees at the left edge on fire
forest.trees[I] = I[1] == 1 ? 2 : 1
end
end
return forest
endforest_fire (generic function with 1 method)Defining the step!
function tree_step!(forest)
# Find trees that are burning (coded as 2)
for I in findall(isequal(2), forest.trees)
for idx in nearby_positions(I.I, forest)
# If a neighbor is Green (1), set it on fire (2)
if forest.trees[idx...] == 1
forest.trees[idx...] = 2
end
end
# Finally, any burning tree is burnt out (2)
forest.trees[I] = 3
end
return forest.trees
endtree_step! (generic function with 1 method)Running the model
forest = forest_fire()
step!(forest, 1)
count(t == 3 for t in forest.trees) # Number of burnt trees on step 170step!(forest, 10)
count(t == 3 for t in forest.trees) # Number of burnt trees on step 11560Now we can do some data collection as well using an aggregate function percentage:
forest = forest_fire(griddims = (20, 20))
burnt_percentage(f) = count(t == 3 for t in f.trees) / prod(size(f.trees))
mdata = [burnt_percentage]
_, data = run!(forest, 10; mdata)
data| Row | time | burnt_percentage |
|---|---|---|
| Int64 | Float64 | |
| 1 | 0 | 0.0 |
| 2 | 1 | 0.0375 |
| 3 | 2 | 0.065 |
| 4 | 3 | 0.0925 |
| 5 | 4 | 0.1125 |
| 6 | 5 | 0.135 |
| 7 | 6 | 0.16 |
| 8 | 7 | 0.1925 |
| 9 | 8 | 0.215 |
| 10 | 9 | 0.245 |
| 11 | 10 | 0.27 |
Now let's plot the model. We use green for unburnt trees, red for burning and a dark red for burnt.
forest = forest_fire()
step!(forest, 1)
plotkwargs = (
add_colorbar = false,
heatarray = :trees,
heatkwargs = (
colorrange = (0, 3),
colormap = cgrad([:white, :green, :red, :darkred]; categorical = true),
),
)
fig, _ = abmplot(forest; plotkwargs...)
fig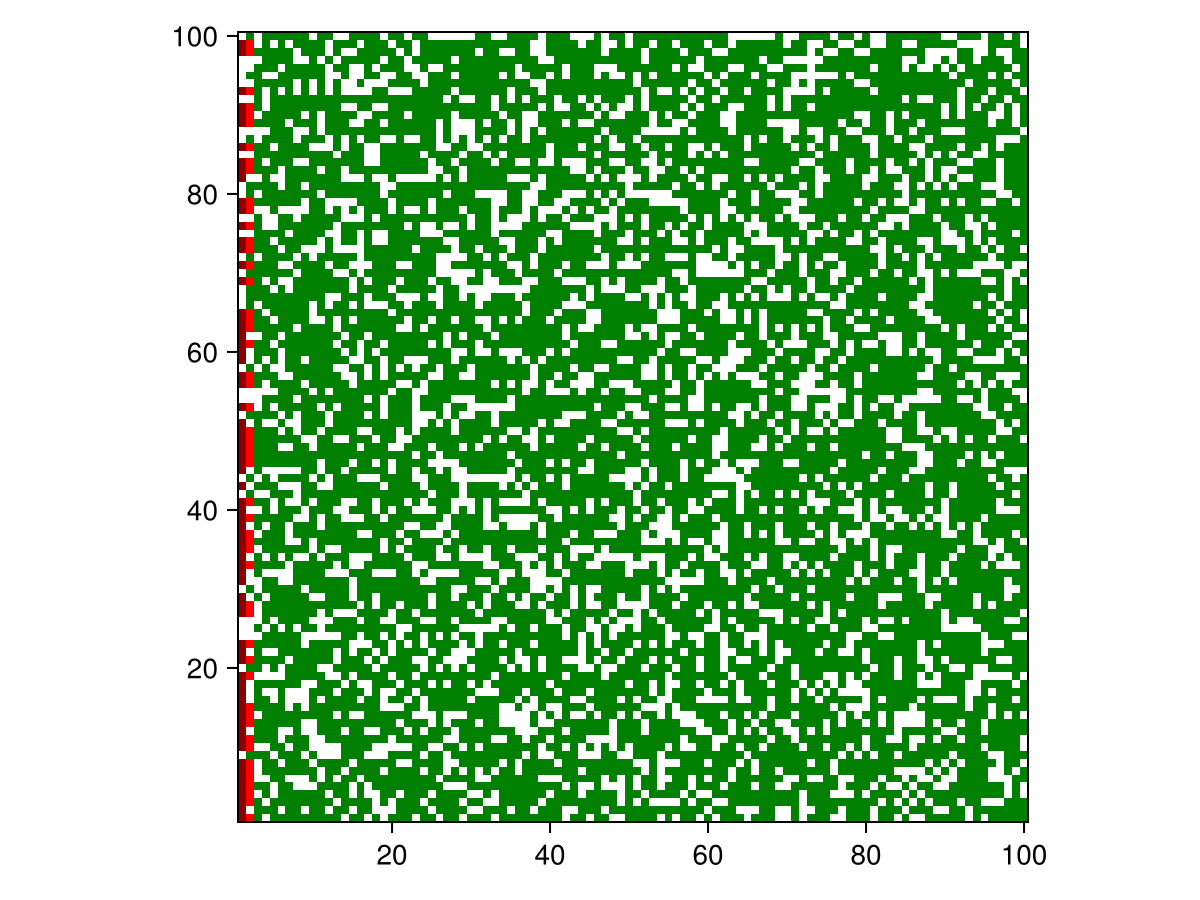
or animate it
forest = forest_fire(density = 0.7, seed = 10)
abmvideo(
"forest.mp4",
forest;
framerate = 5,
frames = 20,
spf = 5,
title = "Forest Fire",
plotkwargs...,
)┌ Warning: keyword `spf` is deprecated in favor of `dt`.
└ @ AgentsVisualizations ~/.julia/packages/Agents/oU8Ee/ext/AgentsVisualizations/src/convenience.jl:102