Full API

States

Use BellState to represent a tensor product of Bell states.

We can represent only Bell states. Here is the basis being used:

`BPGates` notation	Stabilizer tableaux	Kets	in X basis	in Y basis
`00`	`+XX +ZZ`	`∣00⟩+∣11⟩`	`∣++⟩+∣--⟩`	`∣i₊i₋⟩+∣i₋i₊⟩`
`01`	`+XX -ZZ`	`∣01⟩+∣10⟩`	`∣++⟩-∣--⟩`	`∣i₊i₊⟩-∣i₋i₋⟩`
`10`	`-XX +ZZ`	`∣00⟩-∣11⟩`	`∣+-⟩+∣-+⟩`	`∣i₊i₊⟩+∣i₋i₋⟩`
`11`	`-XX -ZZ`	`∣01⟩-∣10⟩`	`∣+-⟩-∣-+⟩`	`∣i₊i₋⟩-∣i₋i₊⟩`

You can convert between these descriptions using

BPGates to stabilizer state with QuantumClifford.Stabilizer(bpgates_state)
stabilizer state to state vector ket with QuantumOptics.Ket

Operations

Most often you would only need CNOTPerm as an operation type. There is a documentation section dedicated to it. It is of the following form:

The most general gate is BellGate. It is built out of smaller gates. It is of the following form:

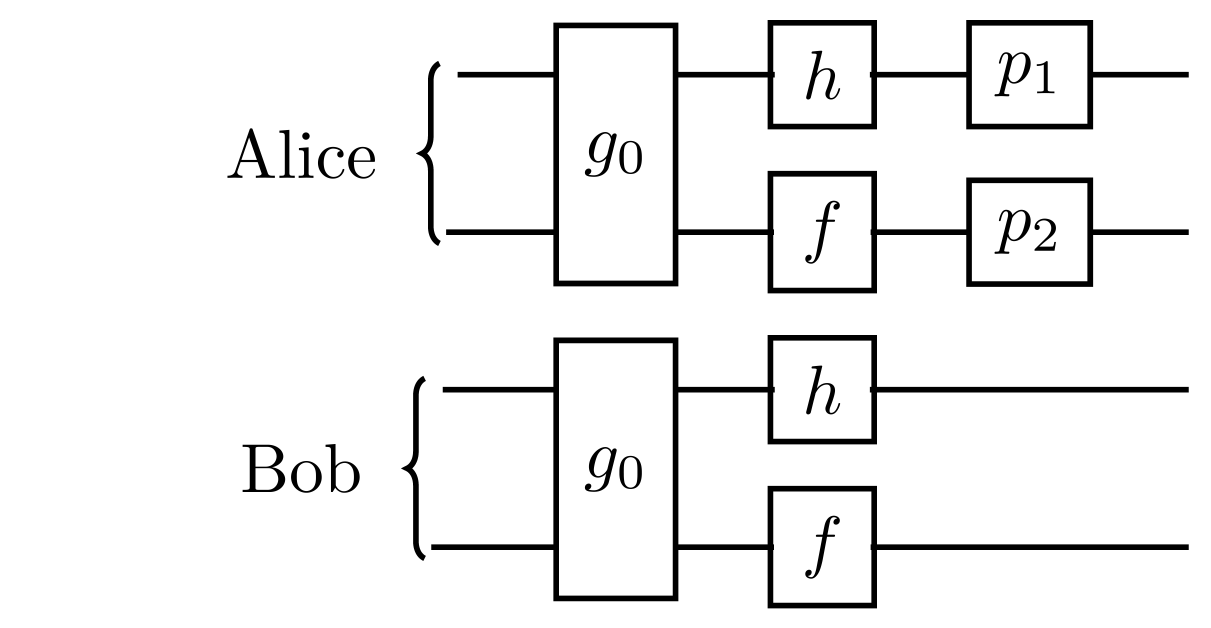
For measurements use BellMeasure which provides coincidence measurements as described in their section of the documentation.

For noisy operations you can use TODO.

The QuantumClifford.apply! function and company (e.g. mctrajectory) can be used for these operations.

Autogenerated API list

BPGates.BellDoublePermutation — Type

Bell preserving gate performing one of 20 possible "Clifford phaseless two-pair permutations" on a two Bell pairs.

Equivalent to applying the same two-qubit Clifford gate to both Alice's and Bob's half-pairs.

The first argument, pidx, specifies the permutation (between 1 and 20). The second argument, sidx indicates which Bell pairs are acted on.

BPGates.BellGate — Type

Most general representation of a Bell preserving gate on two qubits. The general gate consists of a two Pauli permutations, a double qubit permutation, two single qubit permutations, and two indices indicating which pair of Bell states the general Bell preserving gate will be applied to.

BPGates.BellMeasure — Type

Coincidence measurement on Bell pairs.

The first argument, midx, specifies the X, Y, Z basis respectively. The second argument, sidx, indicates which Bell pair is being measured.

The state will be reset to 00 after being applied measurement.

BPGates.BellPauliPermutation — Type

Bell preserving gate performing one of 4 possible "Pauli permutations" on a single Bell pair.

Equivalent to applying a Pauli gate to Alice's side of the Bell pair.

The first argument, pidx, specifies the permutation (between 1 and 4). The second argument, sidx indicates which Bell pair is acted on.

julia> BellPauliPermutation(1,1)*BellState(1) |> Stabilizer
+ XX
+ ZZ

julia> BellPauliPermutation(2,1)*BellState(1) |> Stabilizer
+ XX
- ZZ

julia> BellPauliPermutation(3,1)*BellState(1) |> Stabilizer
- XX
+ ZZ

julia> BellPauliPermutation(4,1)*BellState(1) |> Stabilizer
- XX
- ZZ

BPGates.BellSinglePermutation — Type

Bell preserving gate performing one of 6 possible "Clifford phaseless permutations" on a single Bell pair.

Equivalent to applying certain single-qubit Clifford gates to both Alice and Bob.

The first argument, pidx, specifies the permutation (between 1 and 6). The second argument, sidx indicates which Bell pair is acted on.

BPGates.BellState — Type

A diagonal representation of Bell diagonal states that only tracks the phases in front of the stabilizers tableau instead of the whole stabilizer tableau.

Capable of representing only tensor products of one or more of the states

±XX
±ZZ

by tracking only the phases in the first column. For example, XX -ZZ is represented as the bitstring 01.

This representation permits drastically faster simulation of entanglement purification circuits.

The BellState(n) constructor will create n Bell pairs.

julia> bell_state = BellState([0,1,1,0])
BellState(Bool[0, 1, 1, 0])

julia> Stabilizer(bell_state)
+ XX__
- ZZ__
- __XX
+ __ZZ

As mentioned above, we can represent only Bell states. Here is the basis being used:

`BPGates` notation	Stabilizer tableaux	Kets	in X basis	in Y basis
`00`	`+XX +ZZ`	`∣00⟩+∣11⟩`	`∣++⟩+∣--⟩`	`∣i₊i₋⟩+∣i₋i₊⟩`
`01`	`+XX -ZZ`	`∣01⟩+∣10⟩`	`∣++⟩-∣--⟩`	`∣i₊i₊⟩-∣i₋i₋⟩`
`10`	`-XX +ZZ`	`∣00⟩-∣11⟩`	`∣+-⟩+∣-+⟩`	`∣i₊i₊⟩+∣i₋i₋⟩`
`11`	`-XX -ZZ`	`∣01⟩-∣10⟩`	`∣+-⟩-∣-+⟩`	`∣i₊i₋⟩-∣i₋i₊⟩`

You can convert between these descriptions using

BPGates to stabilizer state with QuantumClifford.Stabilizer(bpgates_state)
stabilizer state to ket with QuantumOptics.Ket

BPGates.CNOTPerm — Type

A bilateral CNOT preceded by permutations on each of the pairs that map the 00 state to itself.

BPGates.GoodSingleQubitPerm — Type

A single-qubit Clifford operation acting as a permutation that maps the 00 state to itself.

BPGates.NoisyBellMeasure — Type

A wrapper for BellMeasure that implements measurement noise.

BPGates.NoisyBellMeasureNoisyReset — Type

A wrapper for BellMeasure that implements measurement noise and Pauli noise after the reset.

BPGates.PauliNoiseBellGate — Type

A wrapper for BellGate that implements Pauli noise in addition to the gate.

BPGates.PauliNoiseOp — Type

PauliNoiseOp(idx,px,py,pz) causes qubit-pair idx to flip to one of the other 3 Bell states with probabilities px, py, pz respectively.

julia> apply!(BellState([0,0]), PauliNoiseOp(1,1,0,0))
BellState(Bool[0, 1])

julia> apply!(BellState([0,0]), PauliNoiseOp(1,0,1,0))
BellState(Bool[1, 1])

julia> apply!(BellState([0,0]), PauliNoiseOp(1,0,0,1))
BellState(Bool[1, 0])

BPGates.bellmeasure! — Method

Apply coincidence measurement on a Bell state.

Return state and measurement result (false if an error is detected).

The measured state will be reset to 00.

julia> bellmeasure!(BellState([0,1,1,1]), BellMeasure(2,1))
(BellState(Bool[0, 0, 1, 1]), false)