Examples
The following examples demonstrate the conceptual operation of Caesar, highlighting specific features of the framework and its use.
Continuous Scalar
Calculating a Square Root (Underdetermined)
Probably the most minimal example that illustrates how factor graphs represent a mathematical framework is a reworking of the classic square root calculation.

WIP, a combined type-definion and square root script is available as an example script. We're working to present the example without having to define any types.
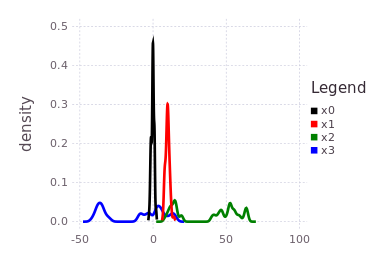
Continuous Scalar with Mixtures
This abstract continuous scalar example illustrates how IncrementalInference.jl enables algebraic relations between stochastic variables, and how a final posterior belief estimate is calculated from several pieces of information.
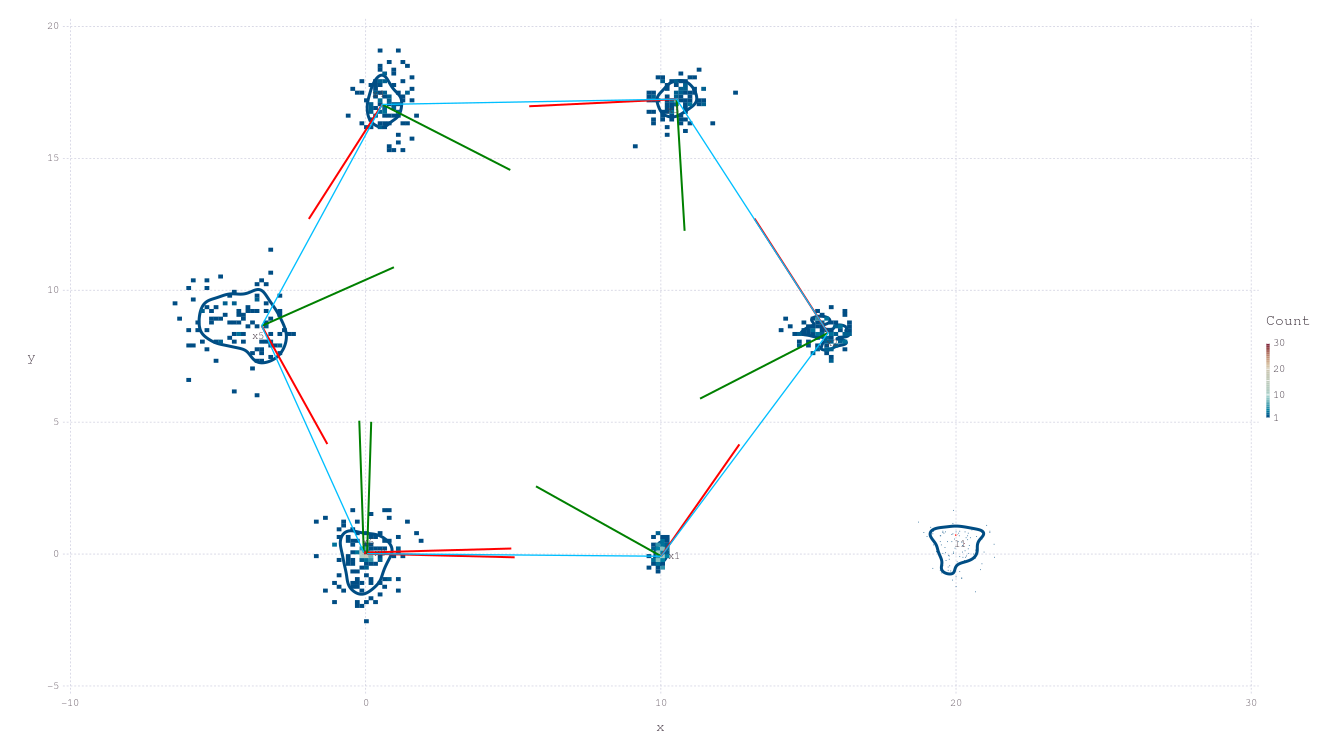
Hexagonal 2D
Batch Mode
A simple 2D hexagonal robot trajectory example is expanded below using techniques developed in simultaneous localization and mapping (SLAM).
Bayes Tree Fixed-Lag Solving - Hexagonal2D Revisited
The hexagonal fixed-lag example shows how tree based clique recycling can be achieved. A further example is given in the real-world underwater example below.
An Underdetermined Solution (a.k.a. SLAM-e-donut)
This tutorial describes (unforced multimodality) a range-only system where there are always more variable dimensions than range measurements made, see Underdeterminied Example here The error distribution over ranges could be nearly anything, but are restricted to Gaussian-only in this example to illustrate an alternative point – other examples show inference results where highly non-Gaussian error distributions are used.
Multi-modal range only example (click here or image for full Vimeo):

Towards Real-Time Underwater Acoustic Navigation
This example uses "dead reckon tethering" (DRT) to perform many of the common robot odometry and high frequency pose updated operations. These features are a staple and standard part of the distributed factor graph system.
Click on image (or this link to Vimeo) for a video illustration:
Uncertain Data Associations, (forced multi-hypothesis)
This example presents a novel multimodal solution to an otherwise intractible multihypothesis SLAM problem. This work spans the entire Victoria Park dataset, and resolves a solution over roughly 10000 variable dimensions with 2^1700 (yes to teh power 1700) theoretically possible modes. At the time of first solution in 2016, a full batch solution took around 3 hours to compute on a very spartan early implementation.
The fractional multi-hypothesis assignments addFactor!(..., multihypo=[1.0; 0.5;0.5]). Similarly for tri-nary or higher multi-hypotheses.
Probabilistic Data Association (Uncertain loop closures)
Example where the standard multihypothesis addFactor!(.., multihypo=[1.0;0.5;0.5]) interface is used. This is from the Kitti driving dataset. Video here. The data association and multihypothesis section discusses this feature in more detail.

Synthetic Aperture Sonar SLAM
The full functional (approximate sum-product) inference approach can be used to natively imbed single hydrophone acoustic waveform data into highly non-Gaussian SAS factors–that implicitly perform beamforming/micro-location–-for a simultaneous localization and mapping solution (image links to video). See the Raw Correlator Probability (Matched Filter) Section for more details.
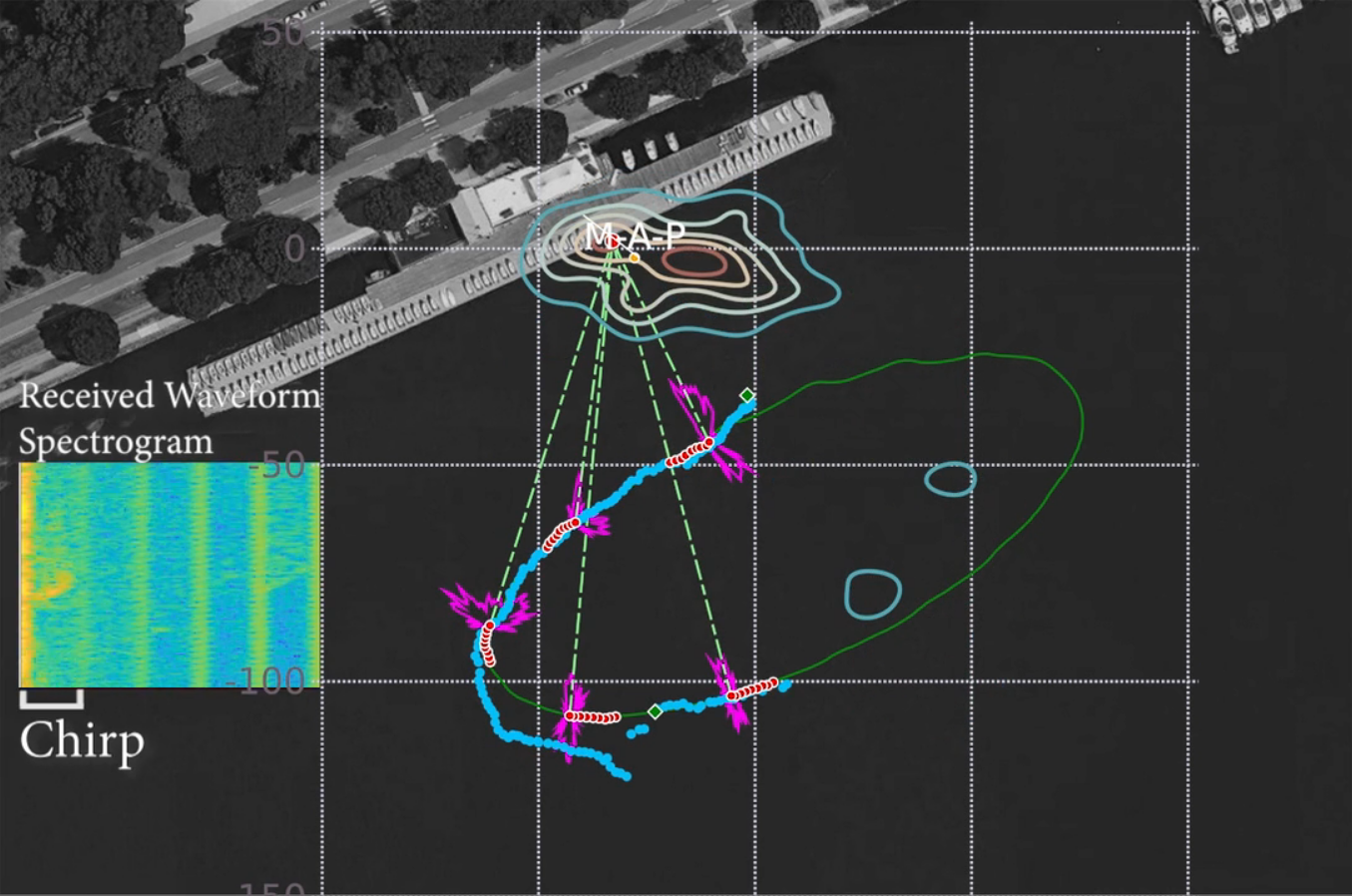
Marine Surface Vehicle with ROS
- New marine surface vehicle code tutorial using ROS.
See initial example here, and native ROS support section here.
Simulated Ambiguous SONAR in 3D
Intersection of ambiguous elevation angle from planar SONAR sensor:
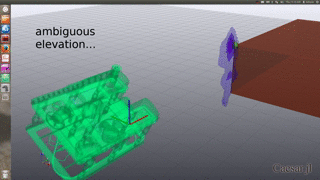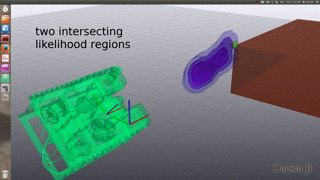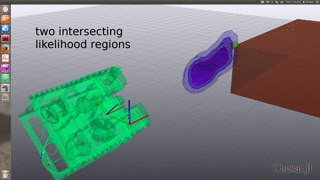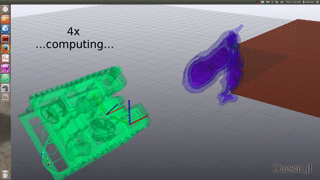
Bi-modal belief
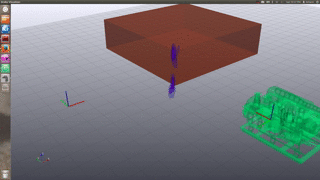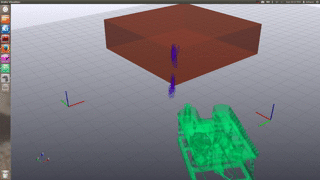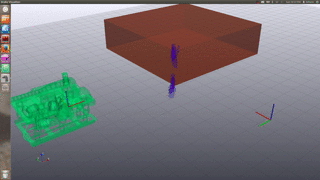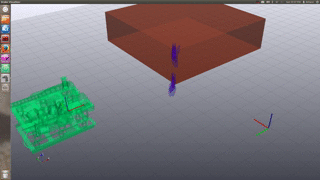
Multi-session Indoor Robot
Multi-session Turtlebot example of the second floor in the Stata Center:
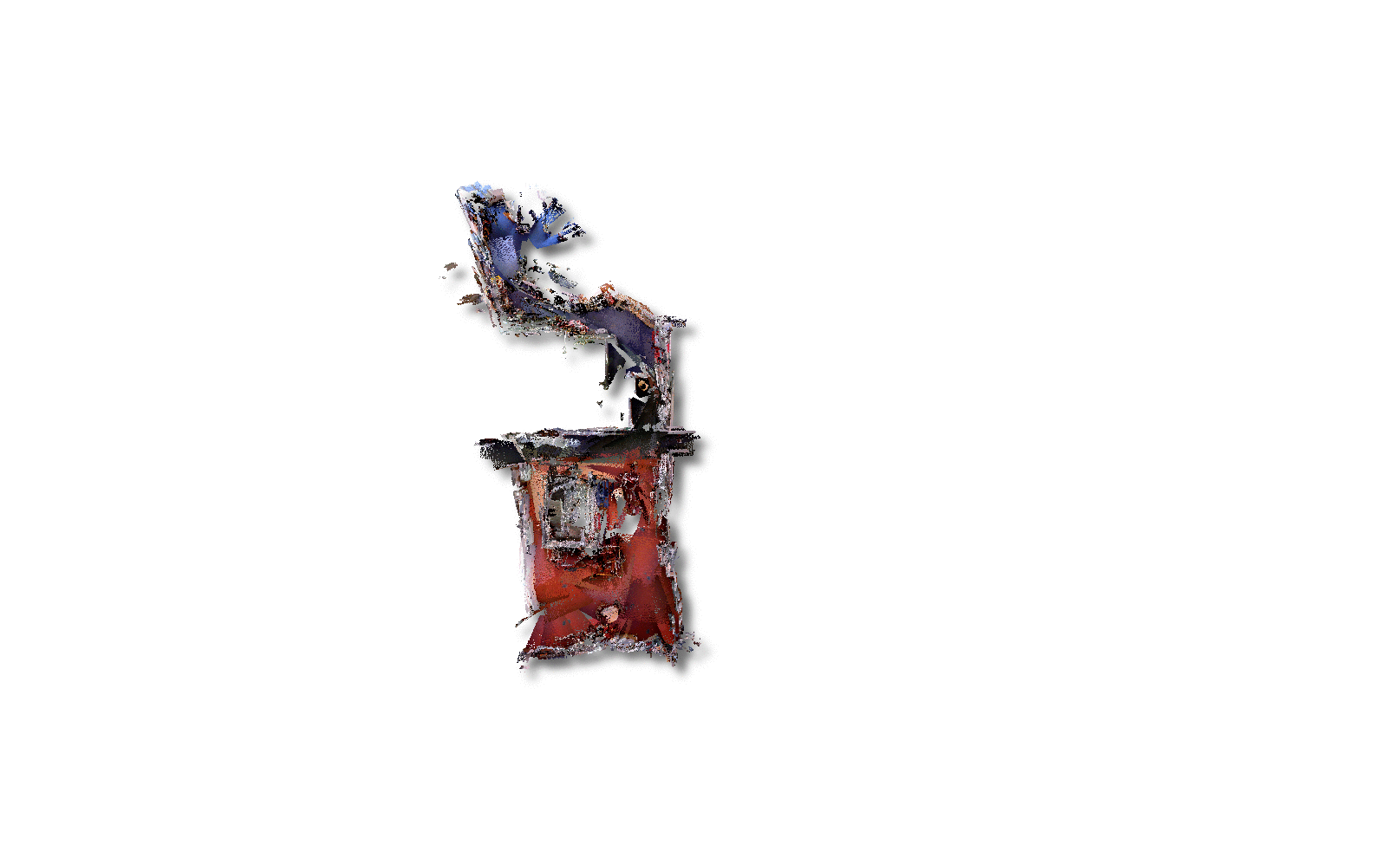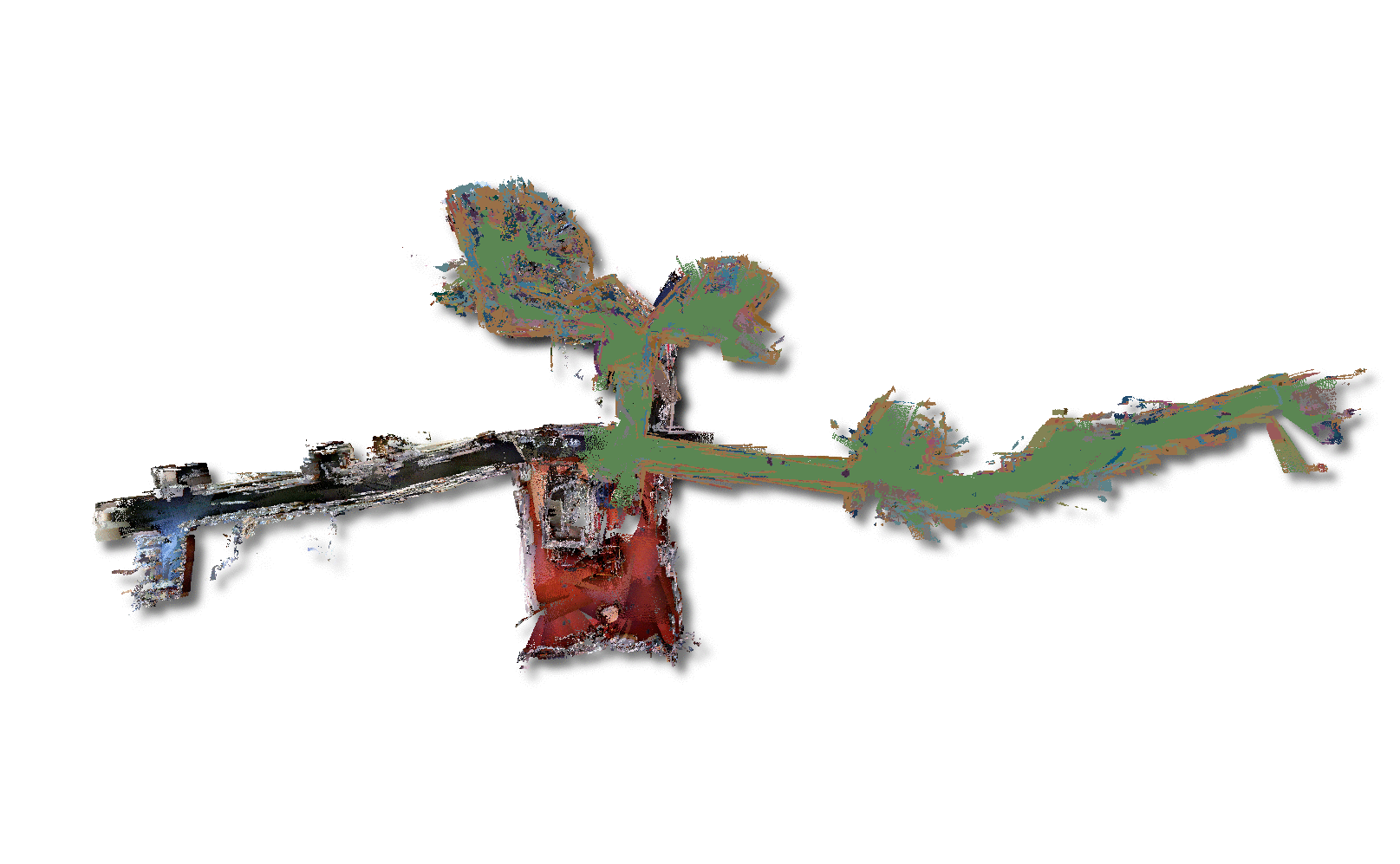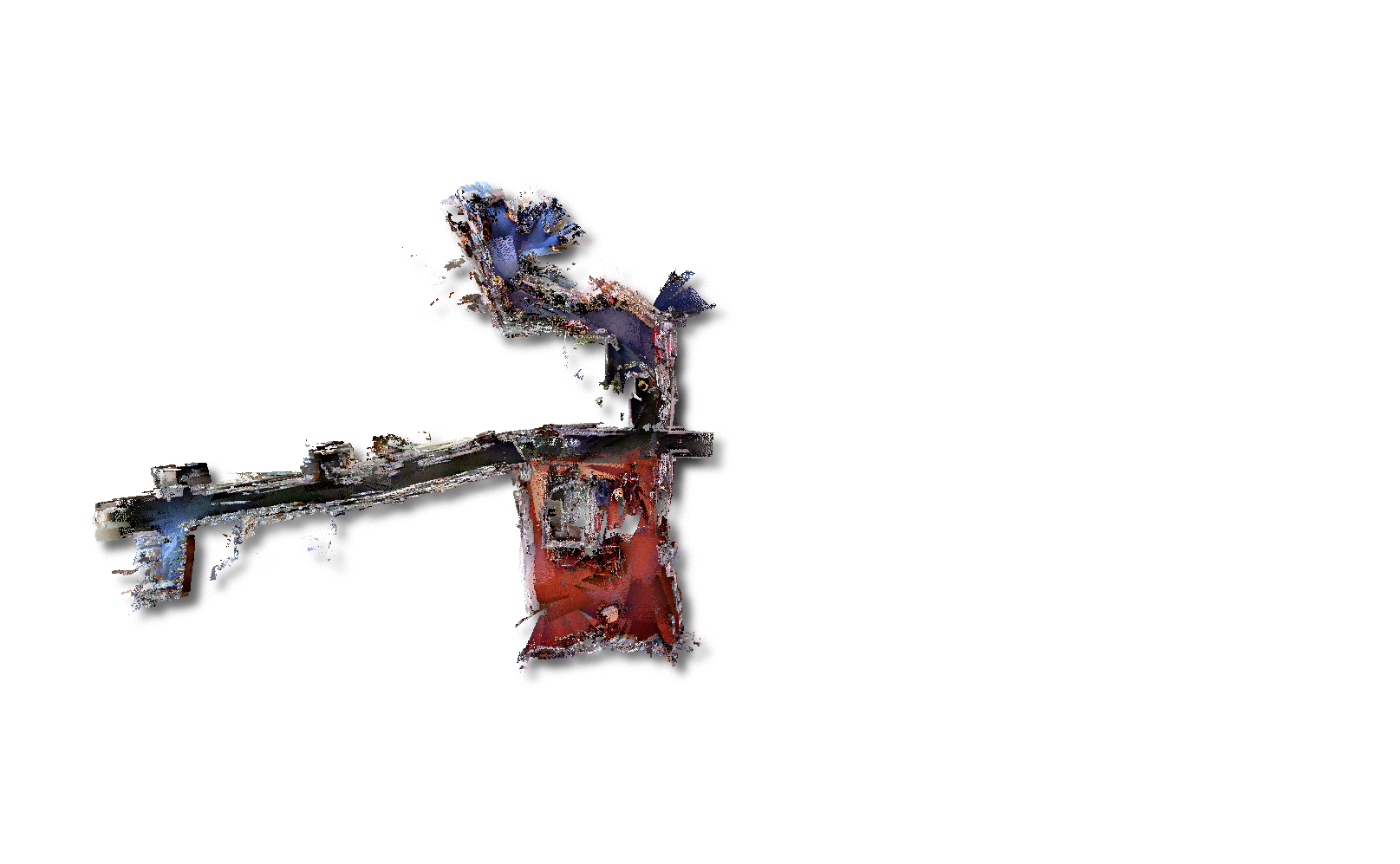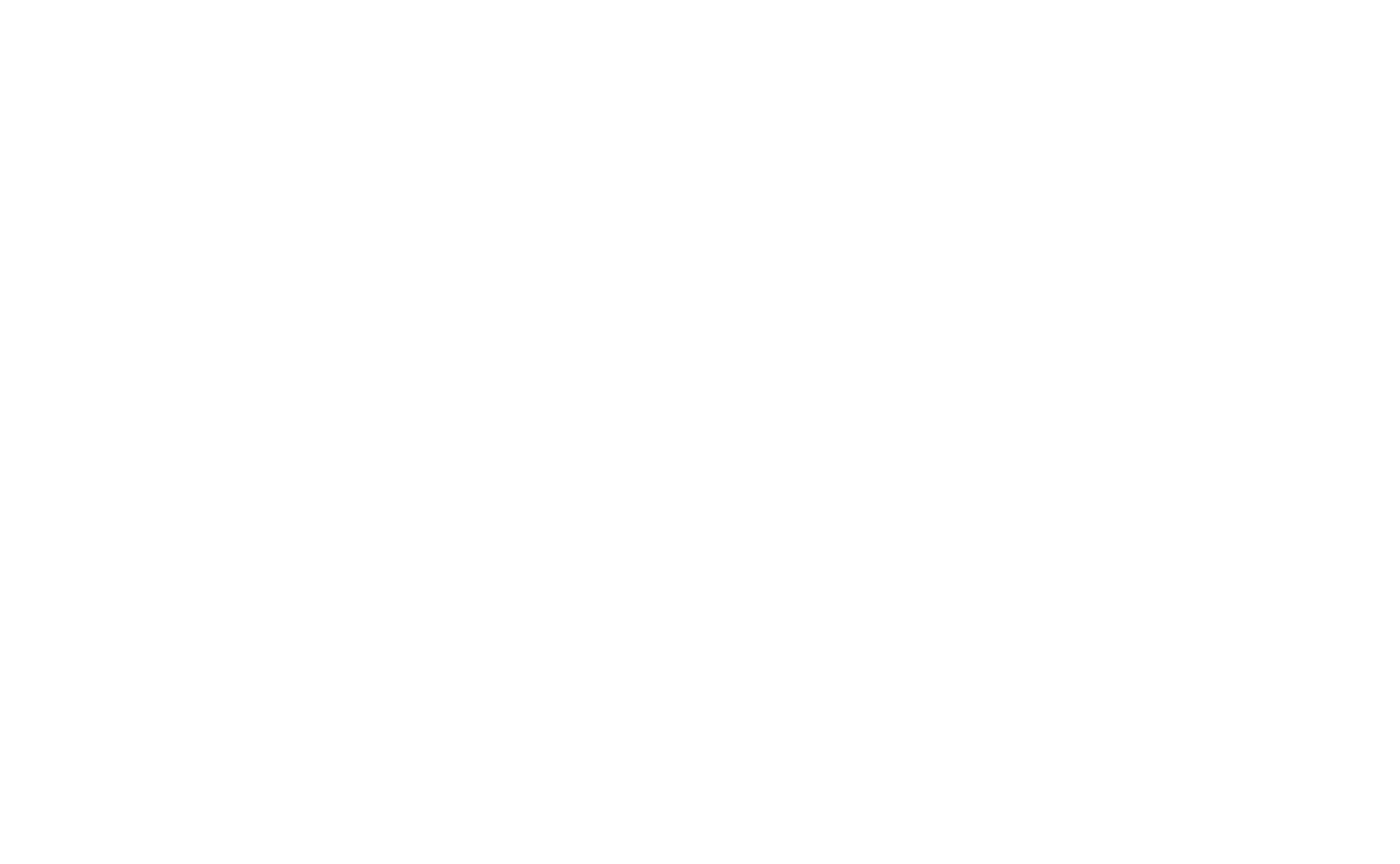
See the multisession information page for more details, as well as academic work:
More Examples
Please see examples folders for Caesar and RoME for more examples, with expanded documentation in the works.
Adding Factors - Simple Factor Design
Caesar can be extended with new variables and factors without changing the core code. An example of this design pattern is provided in this example.
Defining New Variables and Factor