Simple example
Introduction
Here we introduce the main features of the package using a simple example based on the one in the paper published by Pooley et al that described the model-based-proposal (MBP) method, (which is also one of the main inference methods implemented by DiscretePOMP.jl.)
Some familiarity with both Discrete state-space models and Bayesian inference is assumed, but as a brief refresher:
DPOMP (or 'compartmental' models)
Perhaps the most familiar (to most people) example of these are the epidemiological variants, and in particular SIR and closely related SIS model, as illustrated below.
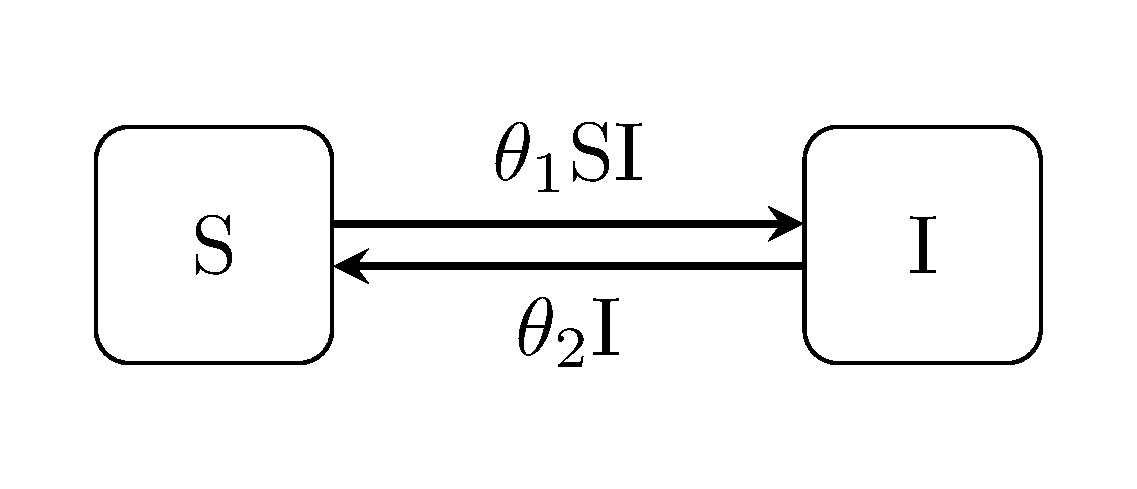
Individuals are assumed to take one of n discrete states –in this case Susceptible or Infectious.
Individuals are also assumed to 'migrate' between states randomly at rates defined as a function of the overall system state. For example, here the rate of the new infections (S -> I) is defined by product of the number of infectious and the number of susceptible individuals, scaled by an unknown contact rate parameter Beta. [ADD GREEK]
Bayesian inference
Defining models
Predefined models
The package includes a set of predefined models, which can be instantiated easily:
julia> import DiscretePOMP # simulation / inference for epidemiological models
julia> import Random # other assorted packages used incidentally
julia> import DataFrames
ERROR: ArgumentError: Package DataFrames not found in current path:
- Run `import Pkg; Pkg.add("DataFrames")` to install the DataFrames package.
julia> import Distributions
ERROR: ArgumentError: Package Distributions not found in current path:
- Run `import Pkg; Pkg.add("Distributions")` to install the Distributions package.
julia> model = generate_model("SIS", [100,1])
ERROR: UndefVarError: generate_model not definedCustomising models
Models can also be specified manually. This is described further in the Models section.
Simulation
The main purpose of the package is to provide an automated framework for parameter inference, described in the next section. However much can also be learned from the use of simulated data; data obtained by generating [i.e. sampling] realisations of the model, generally referred to herein as 'trajectories'. For example, it can be an aid to intuition with respect to the internal dynamics mathematically described by the model, or as a method for predicting system behaviour under certain conditions.
The package implements the Gillespie direct method algorithm for simulation. It can be invoked thusly:
julia> Random.seed!(1)
Random.MersenneTwister(UInt32[0x00000001], Random.DSFMT.DSFMT_state(Int32[1749029653, 1072851681, 1610647787, 1072862326, 1841712345, 1073426746, -198061126, 1073322060, -156153802, 1073567984 … 1977574422, 1073209915, 278919868, 1072835605, 1290372147, 18858467, 1815133874, -1716870370, 382, 0]), [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0 … 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], UInt128[0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000 … 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000, 0x00000000000000000000000000000000], 1002, 0)
julia> theta = [0.003, 0.1]
2-element Array{Float64,1}:
0.003
0.1
julia> x = gillespie_sim(model, theta) # run simulation
ERROR: UndefVarError: gillespie_sim not defined
julia> p = plot_trajectory(x) # plot (optional)
ERROR: UndefVarError: plot_trajectory not defined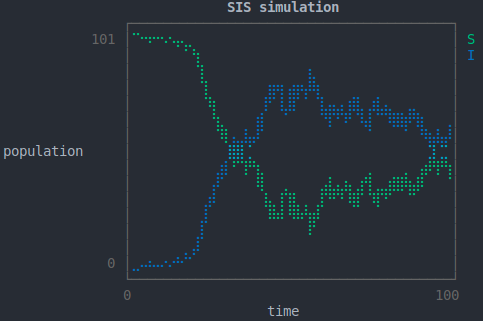
Inference
Here we demonstrate the package's functionality for [single-model] Bayesian inference using two of the algorithms implemented by the package; data-augmented Markov chain Monte Carlo (MCMC), and iterative-batch-importance sampling (IBIS).
First though, it is necessary to define an appropriate prior distribution, using the Distributions package:
julia> model.prior = Distributions.Product(Distributions.Uniform.(zeros(2), [0.1, 0.5]))
ERROR: UndefVarError: Distributions not definedMCMC
The first inference algorithm is MCMC; is a form of rejection sampling. The default number of Markov chains run for an analysis is three, and the Gelman-Rubin convergence diagnostic is carried out by default:
julia> results = run_mcmc_analysis(model, y)
ERROR: UndefVarError: run_mcmc_analysis not defined
julia> tabulate_results(results)
ERROR: UndefVarError: tabulate_results not defined
julia> # trace plot of contact parameter (optional)
println(plot_parameter_trace(results, 1))
ERROR: UndefVarError: plot_parameter_trace not defined
IBIS
The second class of algorithm we demonstrate here, is iterative-batch-importance sampling.
julia> results = run_ibis_analysis(model, y)
ERROR: UndefVarError: run_ibis_analysis not defined
julia> tabulate_results(results)
ERROR: UndefVarError: tabulate_results not definedThe default configuration is particle [filter]-IBIS (i.e. the SMC^2 algorithm) but MBP can be used instead.
Model comparison
Finally, we describe how to compare models using the Bayes factor. First, we define an SEIS model to compare the SIS model/data with:
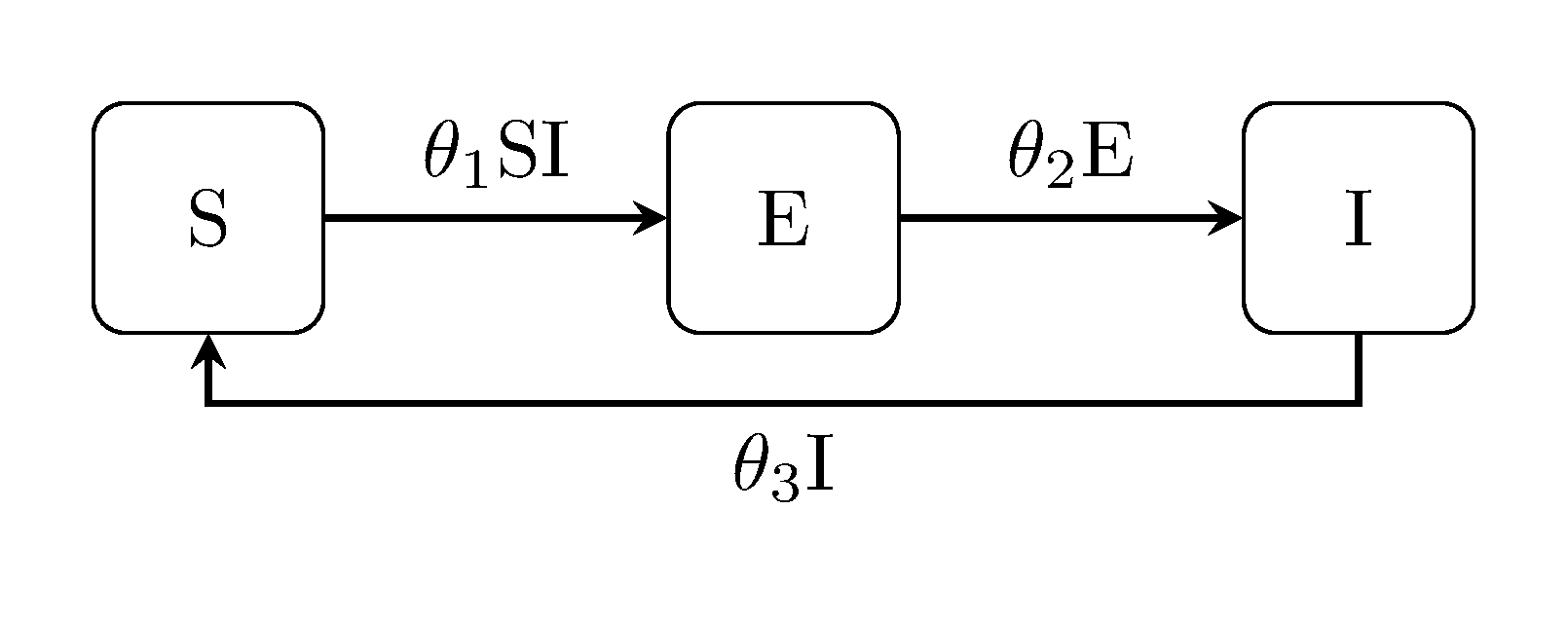
julia> # define model to compare against
seis_model = generate_model("SEIS", [100,0,1])
ERROR: UndefVarError: generate_model not defined
julia> seis_model.prior = Distributions.Product(Distributions.Uniform.(zeros(3), [0.1,0.5,0.5]))
ERROR: UndefVarError: Distributions not defined
julia> seis_model.obs_model = partial_gaussian_obs_model(2.0, seq = 3, y_seq = 2)
ERROR: UndefVarError: partial_gaussian_obs_model not definedseq here denotes the compartment that is observed (i.e. infectious individuals) in the SEIS model state space. Since the observations data y is formatted based on the SIS model, we also specify that column as y_seq.
Finally, we run the comparison, tabulate and plot the results:
julia> # run comparison
models = [model, seis_model]
ERROR: UndefVarError: model not defined
julia> mcomp = run_model_comparison_analysis(models, y)
ERROR: UndefVarError: run_model_comparison_analysis not defined
julia> tabulate_results(mcomp; null_index = 1)
ERROR: UndefVarError: tabulate_results not defined
julia> println(plot_model_comparison(mcomp))
ERROR: UndefVarError: plot_model_comparison not defined