Sampling Random Variables
Fortuna.jl package allows to easily generate samples of both uncorrelated and correlated random variables using rand() function using different sampling techniques. Current version of the package implements Inverse Transform Sampling (ITS) and Latin Hypercube Sampling (LHS) techniques.
Sampling Random Variables
To generate samples of a random variable:
- Generate a random variable (
X).
X = randomvariable("Gamma", "M", [10, 1.5])- Sample the generated random variable using a sampling technique of your choice.
XSamples = rand(X, 10000, :LHS)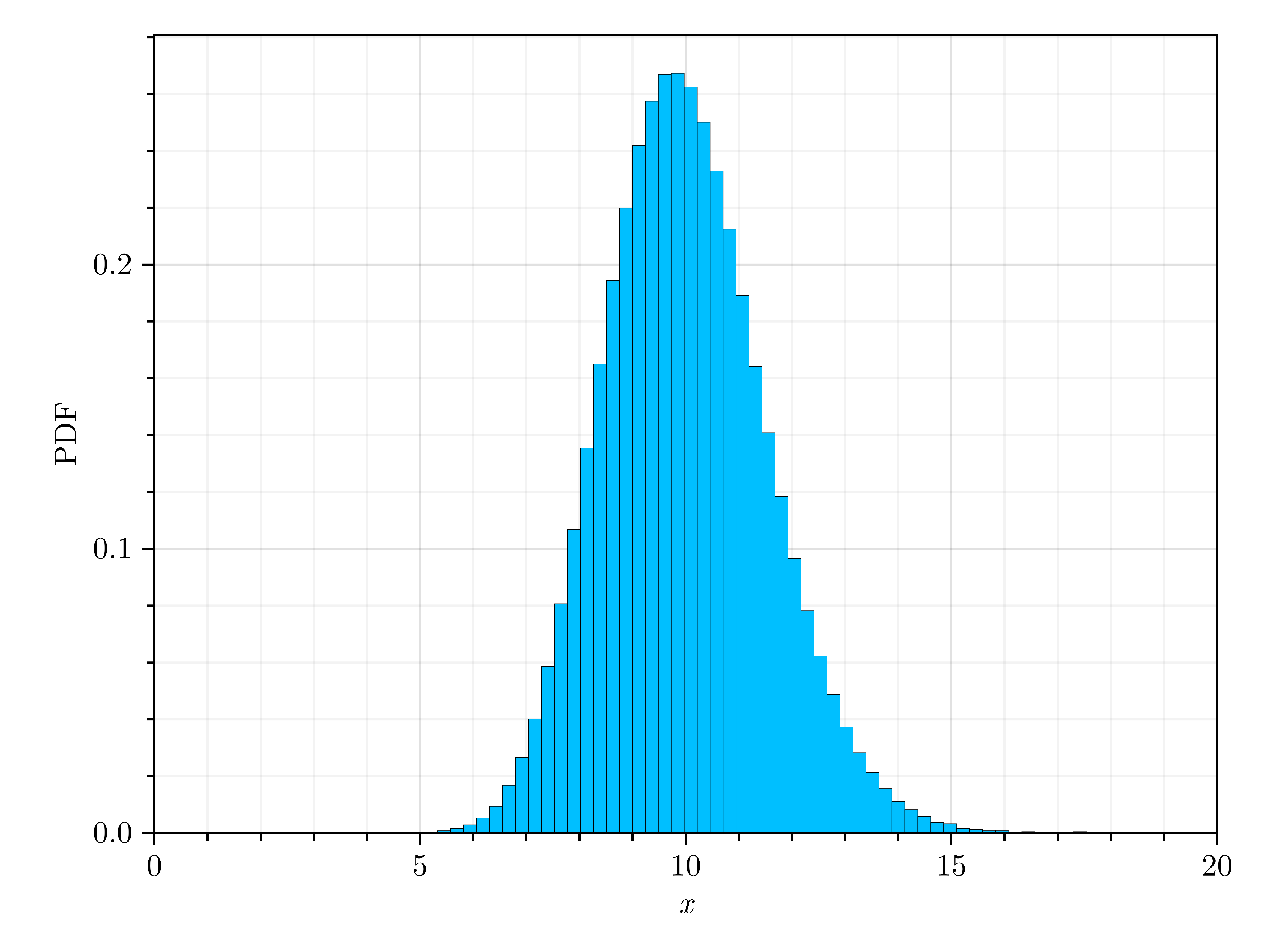
Sampling Random Vectors with Uncorrelated Marginals
To generate samples of a random vector with uncorrelated marginals:
- Generate random variables (
X₁andX₂).
X₁ = randomvariable("Gamma", "M", [10, 1.5])
X₂ = randomvariable("Gamma", "M", [15, 2.5])- Define a random vector (
X) with the generated random variables as marginals.
X = [X₁, X₂]- Sample the defined random vector using a sampling technique of your choice.
XSamples = rand(X, 10000, :LHS)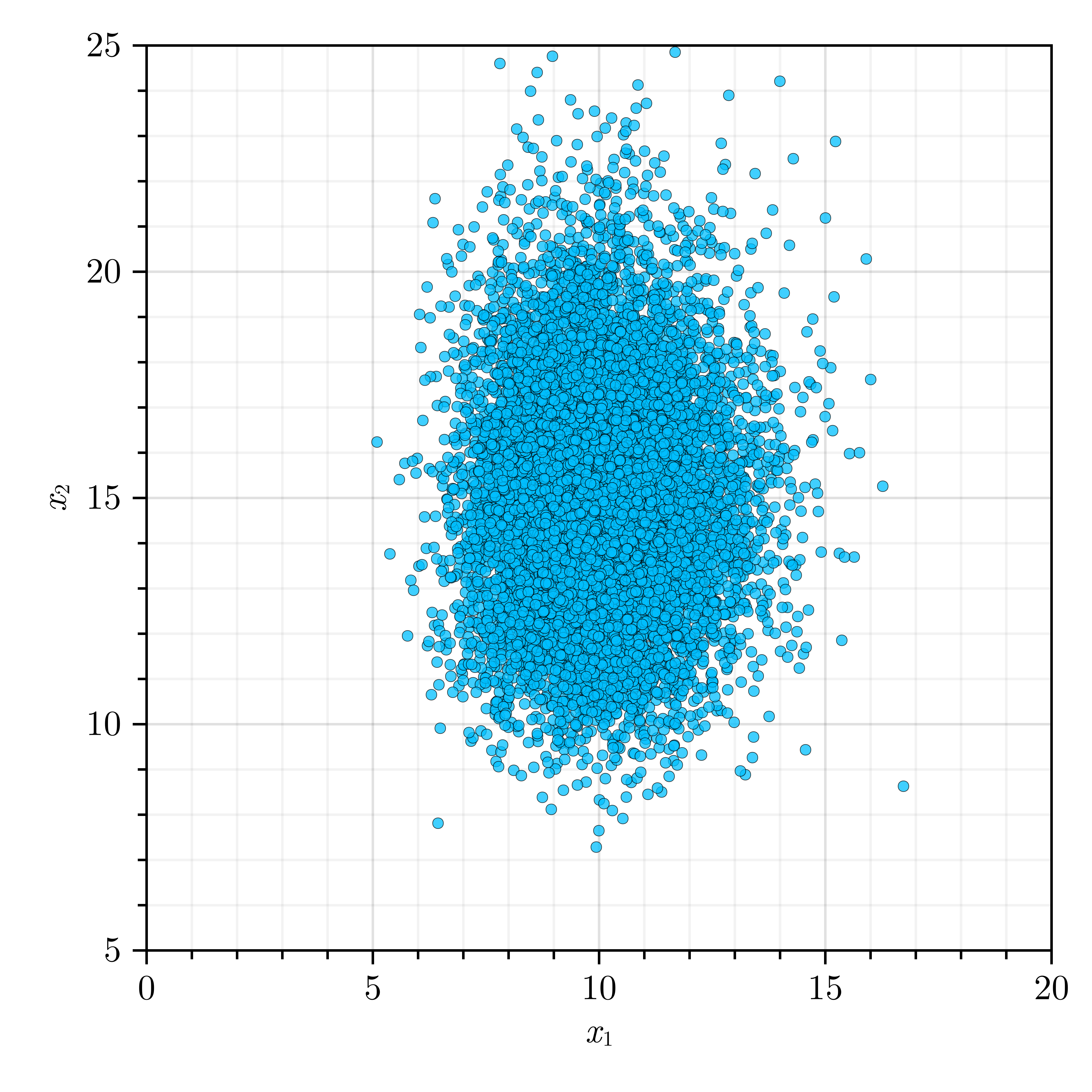
Sampling Random Vectors with Correlated Marginals
When sampling random vectors with correlated marginals, the sampling technique determines how samples are generated in the space of uncorrelated standard normal random variables (referred to as $U$-space). These generated samples are then transformed into the target space of correlated non-normal random variables (referred to as $X$-space). For more information see Nataf Transformation and Rosenblatt Transformation.
To generate samples of a random vector with correlated marginals:
- Generate random variables (
X₁andX₂).
X₁ = randomvariable("Gamma", "M", [10, 1.5])
X₂ = randomvariable("Gamma", "M", [15, 2.5])- Define a random vector (
X) with the generated random variables as marginals.
X = [X₁, X₂]- Define a correlated matrix (
ρˣ) for the defined random vector.
ρˣ = [1 -0.75; -0.75 1]- Define a transformation object that hold all information about the defined random vector.
TransformationObject = NatafTransformation(X, ρˣ)- Sample the defined random vector using a sampling technique of your choice.
XSamples, ZSamples, USamples = rand(TransformationObject, 10000, :LHS)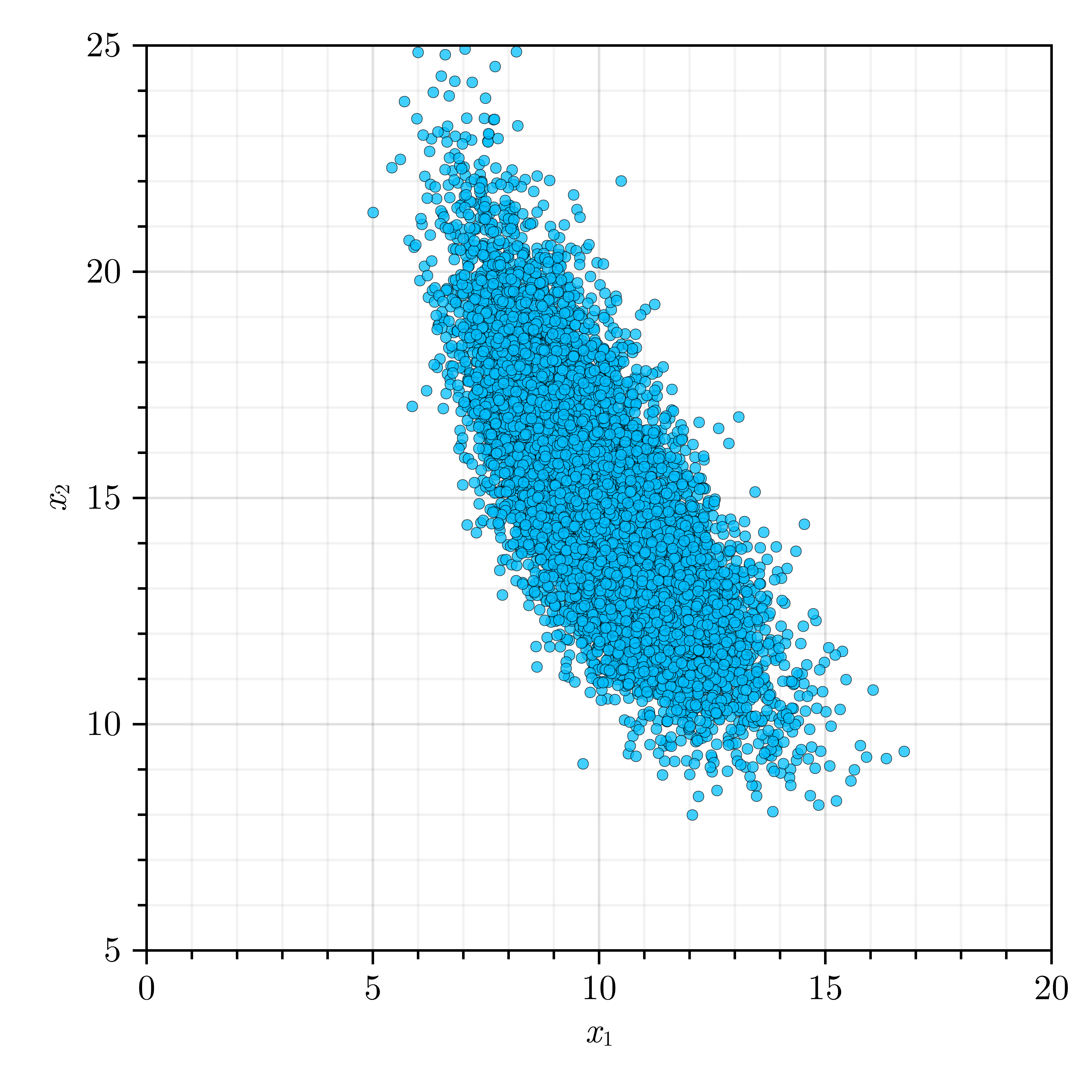
API
Base.rand — Methodrand(RNG::Distributions.AbstractRNG, RandomVariable::Distributions.UnivariateDistribution, NumSamples::Integer, SamplingTechnique::Symbol)Function used to generate samples from an random variable. If SamplingTechnique is:
:ITSsamples are generated using Inverse Transform Sampling technique.:LHSsamples are generated using Latin Hypercube Sampling technique.
Base.rand — Methodrand(RNG::Distributions.AbstractRNG, RandomVector::Vector{<:Distributions.UnivariateDistribution}, NumSamples::Integer, SamplingTechnique::Symbol)Function used to generate samples from a random vector with uncorrelated marginals. If SamplingTechnique is:
:ITSsamples are generated using Inverse Transform Sampling technique.:LHSsamples are generated using Latin Hypercube Sampling technique.
Base.rand — Methodrand(RNG::Distributions.AbstractRNG, TransformationObject::NatafTransformation, NumSamples::Integer, SamplingTechnique::Symbol)Function used to generate samples from a random vector with correlated marginals using Nataf Transformation object. If SamplingTechnique is:
:ITSsamples are generated using Inverse Transform Sampling technique.:LHSsamples are generated using Latin Hypercube Sampling technique.