Getting Started
Installation
The most current, tagged version of GPLinearODEMaker.jl can be easily installed using Julia's Pkg
Pkg.add("GPLinearODEMaker")If you would like to contribute to the package, or just want to run the latest (untagged) version, you can use the following
Pkg.develop("GPLinearODEMaker")Example
Here's an example using sine and cosines as the outputs to be modelled. The f, g!, and h! functions at the end give the likelihood, gradient, and Hessian, respectively.
import GPLinearODEMaker; GLOM = GPLinearODEMaker
kernel, n_kern_hyper = GLOM.include_kernel("se")
n = 100
xs = 20 .* sort(rand(n))
noise1 = 0.1 .* ones(n)
noise2 = 0.2 .* ones(n)
y1 = sin.(xs) .+ (noise1 .* randn(n))
y2 = cos.(xs) .+ (noise2 .* randn(n))
ys = collect(Iterators.flatten(zip(y1, y2)))
noise = collect(Iterators.flatten(zip(noise1, noise2)))
glo = GLOM.GLO(kernel, n_kern_hyper, 2, 2, xs, ys; noise = noise, a=[[1. 0.1];[0.1 1]])
total_hyperparameters = append!(collect(Iterators.flatten(glo.a)), [10])
workspace = GLOM.nlogL_matrix_workspace(glo, total_hyperparameters)
function f(non_zero_hyper::Vector{T} where T<:Real) = GLOM.nlogL_GLOM!(workspace, glo, non_zero_hyper) # feel free to add priors here to optimize on the posterior!
function g!(G::Vector{T}, non_zero_hyper::Vector{T}) where T<:Real
G[:] = GLOM.∇nlogL_GLOM!(workspace, glo, non_zero_hyper) # feel free to add priors here to optimize on the posterior!
end
function h!(H::Matrix{T}, non_zero_hyper::Vector{T}) where T<:Real
H[:, :] = GLOM.∇∇nlogL_GLOM!(workspace, glo, non_zero_hyper) # feel free to add priors here to optimize on the posterior!
endYou can use f, g!, and h! to optimize the GP hyperparameters with external packages like Optim.jl or Flux.jl
initial_x = GLOM.remove_zeros(total_hyperparameters)
using Optim
# @time result = optimize(f, initial_x, NelderMead()) # slow or wrong
# @time result = optimize(f, g!, initial_x, LBFGS()) # faster and usually right
@time result = optimize(f, g!, h!, initial_x, NewtonTrustRegion()) # fastest and usually right
fit_total_hyperparameters = GLOM.reconstruct_total_hyperparameters(glo, result.minimizer)Once you have the best fit hyperparameters, you can easily calculate the GP conditioned on the data (i.e. the GP posterior)
n_samp_points = convert(Int64, max(500, round(2 * sqrt(2) * length(glo.x_obs))))
x_samp = collect(range(minimum(glo.x_obs); stop=maximum(glo.x_obs), length=n_samp_points))
n_total_samp_points = n_samp_points * glo.n_out
n_meas = length(glo.x_obs)
mean_GP, σ, mean_GP_obs, Σ = GLOM.GP_posteriors(glo, x_samp, fit_total_hyperparameters; return_mean_obs=true)and use Plots to visualize the results
using Plots
function make_plot(output::Integer, label::String)
sample_output_indices = output:glo.n_out:n_total_samp_points
obs_output_indices = output:glo.n_out:length(ys)
p = scatter(xs, ys[obs_output_indices], yerror=noise1, label=label)
plot!(x_samp, mean_GP[sample_output_indices]; ribbon=σ[sample_output_indices], alpha=0.3, label="GP")
return p
end
plot(make_plot(1, "Sin"), make_plot(2, "Cos"), layout=(2,1), size=(960,540))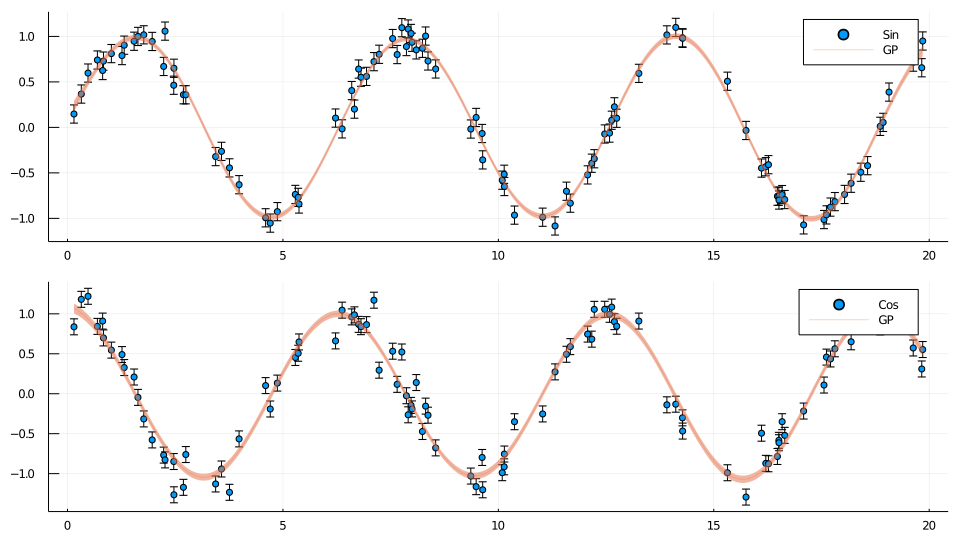
Another, more complicated example where GLOM is used for modelling stellar variability can be found at christiangil/GLOM_RV_Example
Getting Help
To get help on specific functionality you can either look up the information here, or if you prefer you can make use of Julia's native doc-system. For example here's how to get additional information on GPLinearODEMaker.GLO within Julia's REPL:
?GPLinearODEMaker.GLOIf you encounter a bug or would like to participate in the development of this package come find us on Github.