ADCME Basics: Tensor, Type, Operator, Session & Kernel
Tensors and Operators
Tensor is a data structure for storing structured data, such as a scalar, a vector, a matrix or a high dimensional tensor. The name of the ADCME backend, TensorFlow, is also derived from its core framework, Tensor. Tensors can be viewed as symbolic versions of Julia's Array.
A tensor is a collection of $n$-dimensional arrays. ADCME represents tensors using a PyObject handle to the TensorFlow Tensor data structure. A tensor has three important properties
name: Each Tensor admits a unique name.shape: For scalars, the shape is always an empty tuple(); for $n$-dimensional vectors, the shape is(n,); for matrices or higher order tensors, the shape has the form(n1, n2, ...)dtype: The type of the tensors. There is a one-to-one correspondence between most TensorFlow types and Julia types (e.g.,Int64,Int32,Float64,Float32,String, andBool). Therefore, we have overloaded the type name so users have a unified interface.

An important difference is that tensor object stores data in the row-major while Julia's default for Array is column major. The difference may affect performance if not carefully dealt with, but more often than not, the difference is not relevant if you do not convert data between Julia and Python often. Here is a representation of ADCME tensor
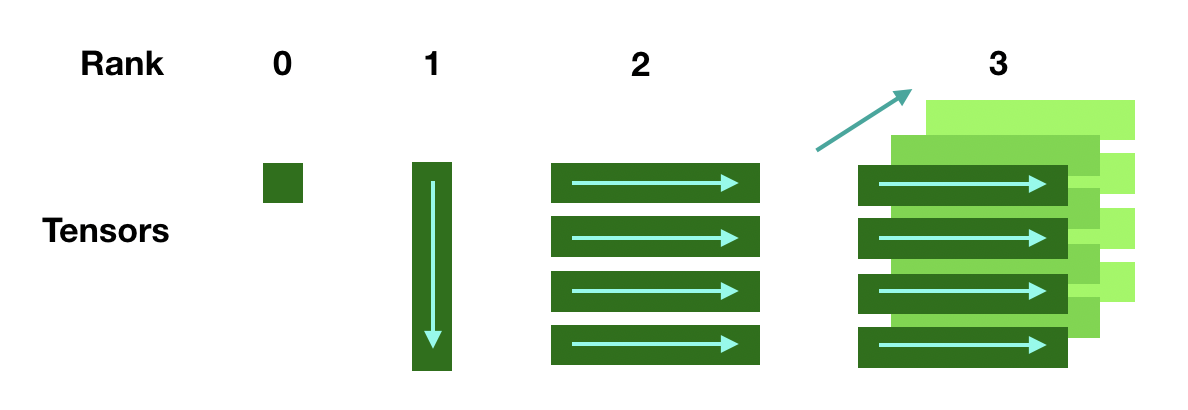
There are 4 ways to create tensors.
constant. As the name suggests,constantcreates an immutable tensor from Julia Arrays.
constant(1.0)
constant(rand(10))
constant(rand(10,10))Variable. In contrast toconstant,Variablecreates tensors that are mutable. The mutability allows us to update the tensor values, e.g., in an optimization procedure. It is very important to understand the difference betweenconstantandVariable: simply put, in inverse modeling, tensors that are defined asVariableshould be the quantity you want to invert, whileconstantis a way to provide known data.
Variable(1.0)
Variable(rand(10))
Variable(rand(10,10))placeholder.placeholderis a convenient way to specify a tensor whose values are to be provided in the runtime. One use case is that you want to try out different values for this tensor and scrutinize the simulation result.
placeholder(Float64, shape=[10,10])
placeholder(rand(10)) # default value is `rand(10)`SparseTensor.SparseTensoris a special data structure to store a sparse matrix. Although it is not very emphasized in machine learning, sparse linear algebra is one of the cores to scientific computing. Thus possessing a strong sparse linear algebra support is the key to success inverse modeling with physics based machine learning.
using SparseArrays
SparseTensor(sprand(10,10,0.3))
SparseTensor([1,2,3],[2,2,2],[0.1,0.3,0.5],3,3) # specify row, col, value, number of rows, number of columnsNow we know how to create tensors, the next step is to perform mathematical operations on those tensors.
Operator can be viewed as a function that takes multiple tensors and outputs multiple tensors. In the computational graph, operators are represented by nodes while tensors are represented by edges. Most mathematical operators, such as +, -, * and /, and matrix operators, such as matrix-matrix multiplication, indexing and linear system solve, also work on tensors.
a = constant(rand(10,10))
b = constant(rand(10))
a + 1.0 # add 1 to every entry in `a`
a * b # matrix vector production
a * a # matrix matrix production
a .* a # element wise production
inv(a) # matrix inversionSession
With the aforementioned syntax to create and transform tensors, we have created a computational graph. However, at this point, all the operations are symbolic, i.e., the operators have not been executed yet.
To trigger the actual computing, the TensorFlow mechanism is to create a session, which drives the graph based optimization (like detecting dependencies) and executes all the operations.
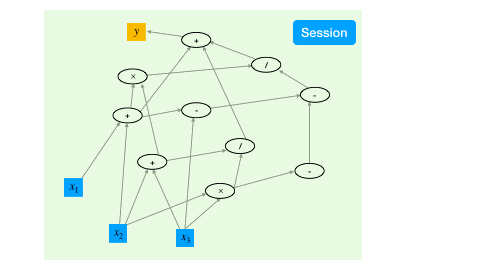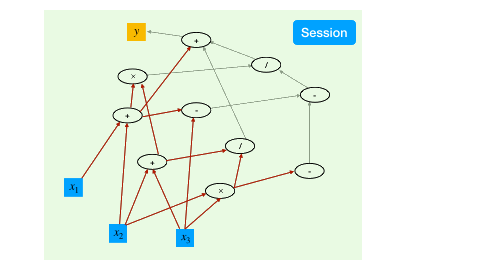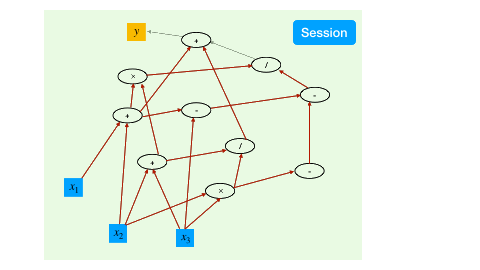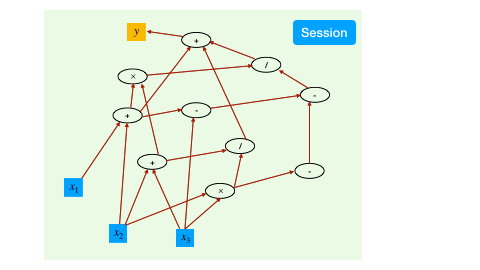
a = constant(rand(10,10))
b = constant(rand(10))
c = a * b
sess = Session()
run(sess, c) # syntax for triggering the execution of the graphIf your computational graph contains Variables, which can be listed via get_collection, then you must initialize your graph before any run command, in which the Variables are populated with initial values
init(sess)Kernel
The kernels provide the low level C++ implementation for the operators. ADCME augments users with missing features in TensorFlow that are crucial for scientific computing and tailors the syntax for numerical schemes. Those kernels, depending on their implementation, can be used in CPU, GPU, TPU or heterogenious computing environments.
All the intensive computations are done either in Julia or C++, and therefore we can achieve very high performance if the logic is done appropriately. For performance critical part, users may resort to custom kernels using customop, which allows you to incooperate custom designed C++ codes.

Summary
ADCME performances operations on tensors. The actual computations are pushed back to low level C++ kernels via operators. A session is need to drive the executation of the computation. It will be easier for you to analyze computational cost and optimize your codes with this computation model in mind.
Tensor Operations
Here we show a list of commonly used operators in ADCME.
| Description | API |
|---|---|
| Constant creation | constant(rand(10)) |
| Variable creation | Variable(rand(10)) |
| Get size | size(x) |
| Get size of dimension | size(x,i) |
| Get length | length(x) |
| Resize | reshape(x,5,3) |
| Vector indexing | v[1:3],v[[1;3;4]],v[3:end],v[:] |
| Matrix indexing | m[3,:], m[:,3], m[1,3],m[[1;2;5],[2;3]] |
| 3D Tensor indexing | m[1,:,:], m[[1;2;3],:,3], m[1:3:end, 1, 4] |
| Index relative to end | v[end], m[1,end] |
| Extract row (most efficient) | m[2], m[2,:] |
| Extract column | m[:,3] |
| Convert to dense diagonal matrix | diagm(v) |
| Convert to sparse diagonal matrix | spdiag(v) |
| Extract diagonals as vector | diag(m) |
| Elementwise multiplication | a.*b |
| Matrix (vector) multiplication | a*b |
| Matrix transpose | m' |
| Dot product | sum(a*b) |
| Solve | A\b |
| Inversion | inv(m) |
| Average all elements | mean(x) |
| Average along dimension | mean(x, dims=1) |
| Maximum/Minimum of all elements | maximum(x), minimum(x) |
| Squeeze all single dimensions | squeeze(x) |
| Squeeze along dimension | squeeze(x, dims=1), squeeze(x, dims=[1;2]) |
| Reduction (along dimension) | norm(a), sum(a, dims=1) |
| Elementwise Multiplication | a.*b |
| Elementwise Power | a^2 |
| SVD | svd(a) |
A[indices] = updates | A = scatter_update(A, indices, updates) |
A[indices] += updates | A = scatter_add(A, indices, updates) |
A[indices] -= updates | A = scatter_sub(A, indices, updates) |
A[idx, idy] = updates | A = scatter_update(A, idx, idy, updates) |
A[idx, idy] += updates | A = scatter_add(A, idx, idy, updates) |
A[idx, idy] -= updates | A = scatter_sub(A, idx, idy, updates) |
In some cases you might find some features missing in ADCME but present in TensorFlow. You can always use tf.<function_name>. It's compatible.