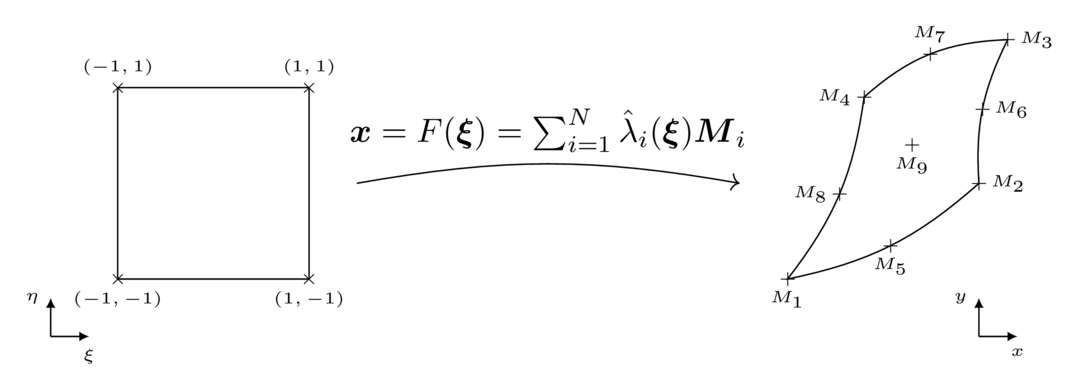Geometry and mesh

A Mesh is a set basically of nodes (Node), a set of entities (the mesh elements) and a list of connectivies that link the entities between themselves and with the nodes.

In Bcube every mesh entity has corresponding reference Shape, a simplified or canonical representation of this element. A 1D line is mapped on the [-1,1] segment, and a rectangle is mapped on a square for instance. On these reference shapes, (almost) everything is known : the vertices location, the area, the quadrature points... Hence in Bcube we always compute things in the reference shape. For "Lagrange" elements (such as Bar*_t, Tri*_t, Quad*_t, Tetra*_t, Hexa*_t, Penta*_t etc), the mapping from the reference shape to a geometrical element is directly obtained from the corresponding Lagrange polynomials and the element node coordinates. Given a geometrical element with n nodes M_i, the mapping reads:

\[F(\xi) = \sum_{i=1}^n \hat{\lambda}_i(\xi)M_i\]

where $(\lambda)_i$ are the Lagrange polynomials whose order matches the element order.