WARNING
Please note that I recently discovered a few bugs that made the examples in this document appear better then they actually are! Woops! The syntax is still useful and the examples as well - but don't feel bad if you don't get the same results. I'll update this when I can...
Curve Resolution Demo
ChemometricsTools has some curve resolution methods baked in. So far NMF, SIMPLISMA, and MCR-ALS are included. If you aren't familiar with them, they are used to extract spectral and concentration estimates from unknown mixtures in chemical signals. Below is an example of spectra which are composed of signals from a mixture of a 3 components. I could write a volume analyzing this simple set, but this is just a show-case of some methods and how to call them, what kind of results they might give you. The beauty of this example is that, we know what is in it, in a forensic or real-world situation we won't know what is in it, and we have to rely on domain knowledge, physical reasoning, and metrics to determine the validity of our results.
Anyways, because we know, the pure spectra look like the following: 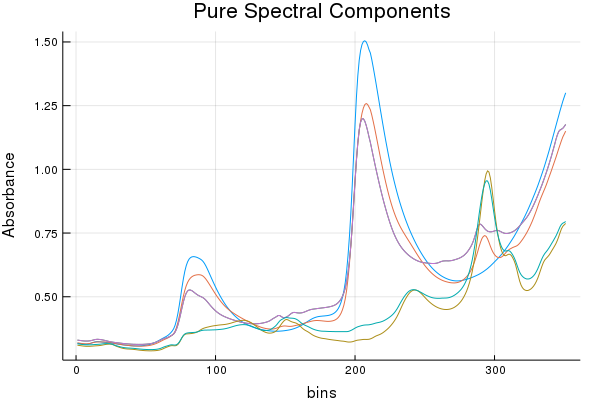
Note: There are three components (water, acetic acid, methanol), but their spectra were collected in duplicate.
And the concentration profiles of the components follow the following simplex design, 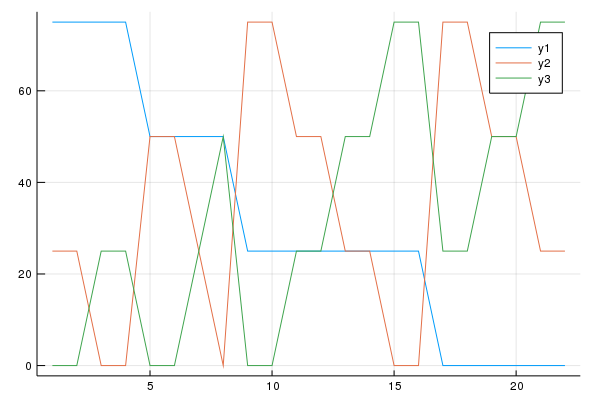
But the models we are using will only see the following (no pure components) 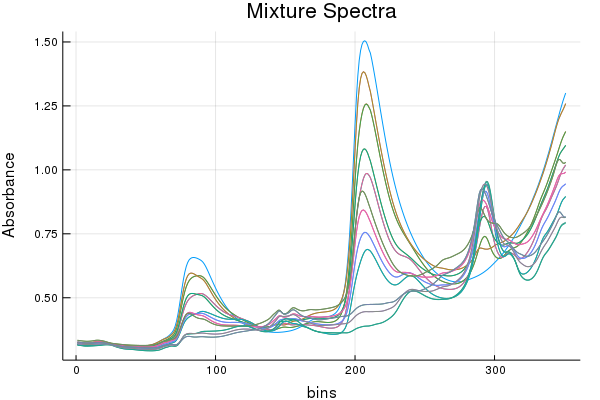
Raw = CSV.read("/triliq.csv");
Mixture = collect(convert(Array, Raw)[:,1:end]);
pure = [10,11,20,21,28,29];
PURE = Mixture[pure,:];
impure = [collect(1:9); collect(12:19);collect(22:27)];
Mixture = Mixture[impure,:];Great, so now let's run NMF, SIMPLISMA, and MCR-ALS with the SIMPLISMA estimates.
( W_NMF, H_NMF ) = NMF(Mixture; Factors = 3, maxiters = 300, tolerance = 1e-8)
(C_Simplisma,S_Simplisma, vars) = SIMPLISMA(Mixture; Factors = 18)
vars
#Find purest variables that are not neighbors with one another
cuts = S_Simplisma[ [1,3,17], :];
( C_MCRALS, S_MCRALS, err ) = MCRALS(Mixture, nothing, RangeNorm(cuts')(cuts')';
Factors = 3, maxiters = 10,
norm = (true, false),
nonnegative = (true, true) )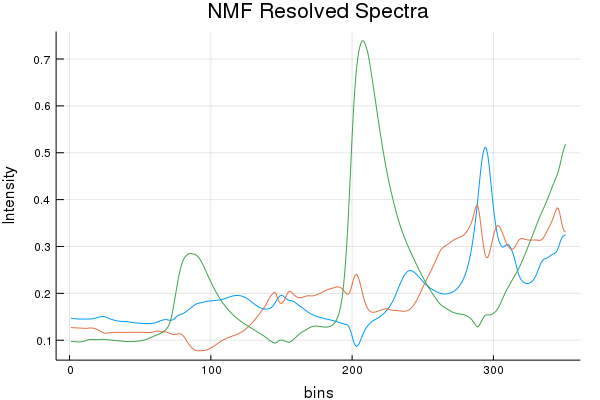
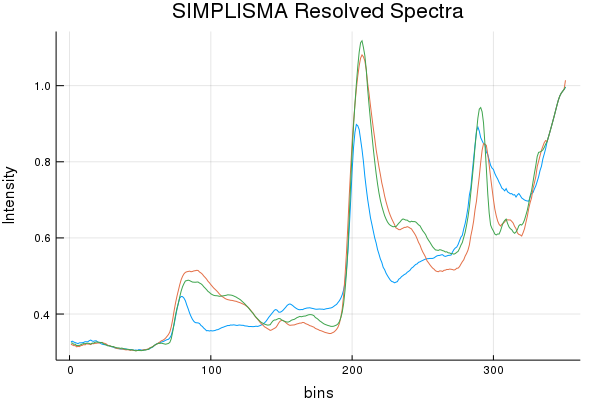
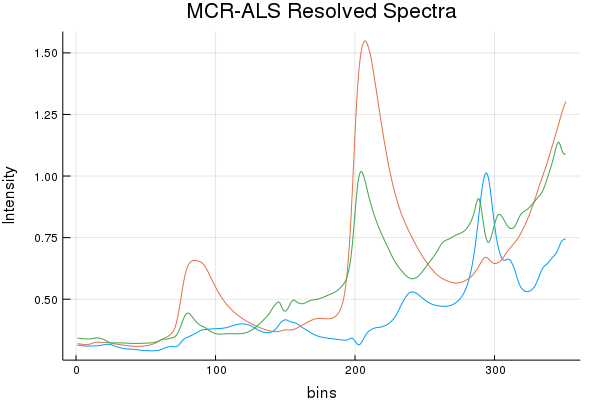
Spectral Recovery Discussion (Results by Eye):
As we can see, NMF does resolve a few components that resemble a few of the actual pure components, but it really butchers the 3rd. While SIMPLISMA does a good job, at finding spectra that look "real" there are characteristics missing from the true spectra. It must be stated; SIMPLISMA wasn't invented for NIR signals. Finding pure variables in dozens... err... hundreds of over-lapping bands isn't really ideal. However, MCR-ALS quickly made work of those initial SIMPLISMA estimates and seems to have found some estimates that somewhat closely resemble the pure components.
Concentration Profile Discussion (Results by Eye):
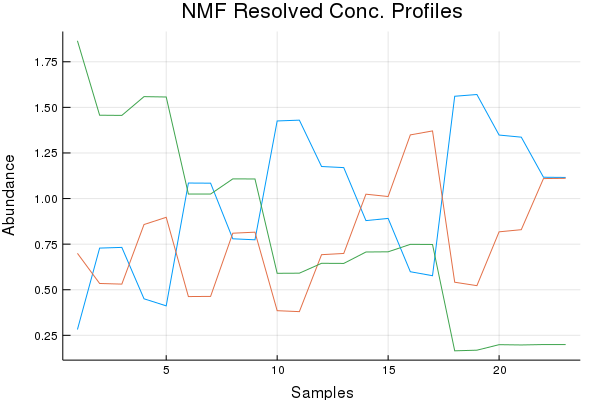
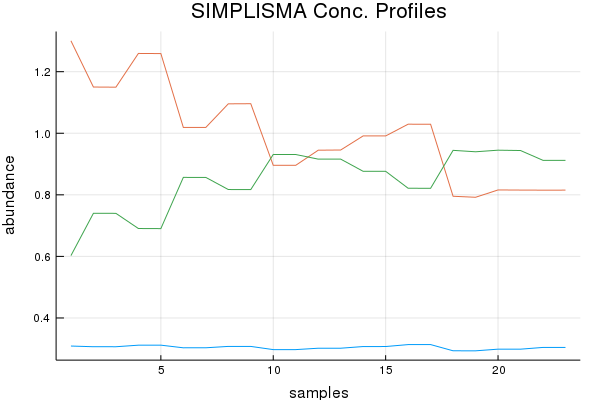
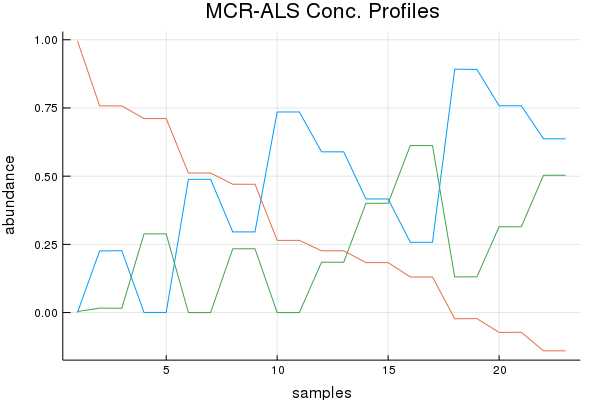
SIMPLISMA basically botched this dataset with regards to the concentration profiles. While NMF and MCR-ALS do quite good. Of course preprocessing can help here, and tinkering too. Ultimately not bad, given the mixture components. I do have a paper that shows another approach to this problem doubtful I'd be allowed to rewrite the code, I think my previous university owns it!
Casey Kneale, Steven D. Brown, Band target entropy minimization and target partial least squares for spectral recovery and quantitation, Analytica Chimica Acta, Volume 1031, 2018, Pages 38-46, ISSN 0003-2670, https://doi.org/10.1016/j.aca.2018.07.054.