Pipelines Demo
Multiple Transformations can be easily chained together and stored using "Pipelines". Preprocessing methods, or really any univariate function may be included in a pipeline, but that will likely mean it can no longer be inverted. Pipelines are basically convenience functions, but are somewhat flexible and can be used for automated searches,
PreprocessPipe = Pipeline(FauxSpectra1, RangeNorm, Center);
Processed = PreprocessPipe(FauxSpectra1);Of course pipelines of transforms can also be inverted,
RMSE( FauxSpectra1, PreprocessPipe(Processed; inverse = true) ) < 1e-14Pipelines can also be created and executed as an 'in place' operation for large datasets. This has the advantage that your data is transformed immediately without making copies in memory. This may be useful for large datasets and memory constrained environments. WARNING: be careful to only run the pipeline call or its inverse once! It is much safer to use the not inplace function outside of a REPL/script environment.
FauxSpectra = randn(10,200);
OriginalCopy = copy(FauxSpectra);
InPlacePipe = PipelineInPlace(FauxSpectra, Center, Scale);See without returning the data or an extra function call we have transformed it according to the pipeline as it was instantiated...
FauxSpectra == OriginalCopy
#Inplace transform the data back
InPlacePipe(FauxSpectra; inverse = true)
RMSE( OriginalCopy, FauxSpectra ) < 1e-14Pipelines are kind of flexible. We can put nontransform (operations that cannot be inverted) preprocessing steps in them as well. In the example below the first derivative is applied to the data, this irreversibly removes a column from the data,
PreprocessPipe = Pipeline(FauxSpectra1, FirstDerivative, RangeNorm, Center);
Processed = PreprocessPipe(FauxSpectra1);
#This should be equivalent to the following...
SpectraDeriv = FirstDerivative(FauxSpectra1);
Alternative = Pipeline(SpectraDeriv , RangeNorm, Center);
Processed == Alternative(SpectraDeriv)Great right? Well what happens if we try to do the inverse of our pipeline with an irreversible function (First Derivative) in it?
PreprocessPipe(Processed; inverse = true)Well we get an assertion error.
Automated Pipeline Example
We can take advantage of how pipelines are created; at their core they are tuples of transforms/functions. So if we can make an array of transforms and set some conditions they can be stored and applied to unseen data. A fun example of an automated transform pipeline is in the whimsical paper written by Willem Windig et. al. That paper is called 'Loopy Multiplicative Scatter Transform'. Below I'll show how we can implement that algorithm here (or anything similar) with ease. Loopy MSC: A Simple Way to Improve Multiplicative Scatter Correction. Willem Windig, Jeremy Shaver, Rasmus Bro. Applied Spectroscopy. 2008. Vol 62, issue: 10, 1153-1159
First let's look at the classic Diesel data before applying Loopy MSC 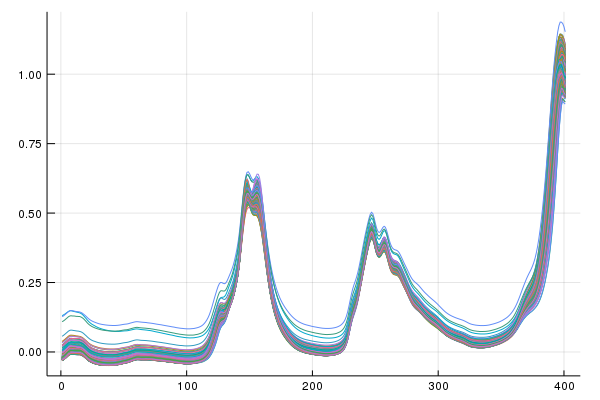
Alright, there is scatter, let's go for it,
RealSpectra = convert(Array, CSV.read("/diesel_spectra.csv"));
Current = RealSpectra;
Last = zeros(size(Current));
TransformArray = [];
while RMSE(Last, Current) > 1e-5
if any(isnan.(Current))
break
else
push!(TransformArray, MultiplicativeScatterCorrection( Current ) )
Last = Current
Current = TransformArray[end](Last)
end
end
#Now we can make a pipeline object from the array of stored transforms
LoopyPipe = Pipeline( Tuple( TransformArray ) );For a sanity check we can ensure the output of the algorithm is the same as the new pipeline so it can be applied to new data.
Current == LoopyPipe(RealSpectra)Looks like our automation driven pipeline is equivalent to the loop it took to make it. More importantly did we remove scatter after 3 automated iterations of MSC? 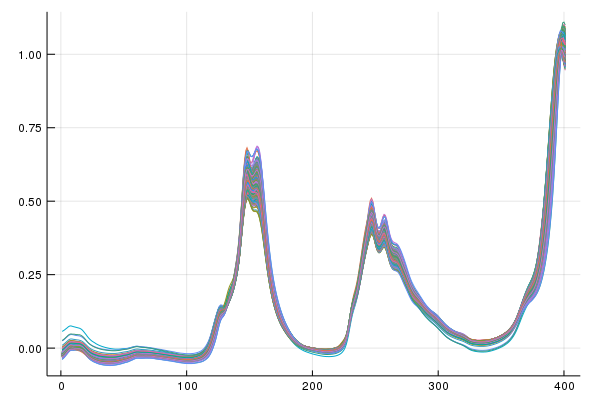
Yes, yes we did. Pretty easy right?