Meshing
In the text terminal, objects are displayed as a CSG tree. To view them graphically, load a Makie back-end (e.g. use GLMakie) and call the Makie.plot command.
Objects are converted to explicit meshes for display or export as STL or SVG files.
The plot, stl, svg commands all perform implicit conversion to meshes; the package is useable without explicit call to the meshing functions. However, working with explicit meshes allows to e.g. perform arbitrary (non-linear) coordinate transformations on the objects.
Plotting
This package defines methods for the Makie.plot function for all CSG objects. Volumes are represented as a triangulated mesh (with faces colored in the appropriate color); two-dimensional shapes are represented as filled polygons (colored in the default color).
It is possible to display the objects either interactively with GLMakie, or as static images with CairoMakie; the latter is what is used to build the examples in this documentation.
Parameters
The meshing of objects is governed by a few parameters:
atolandrtoldetermine the number of faces inserted in the mesh;symmetryallows to impose a given rotational symmetry to circles and cylinders.
To set values other than the defaults for an object, apply the set_parameters transform to that object:
set_parameters(atol=1)*
circle(2)julia> s = union(set_parameters(atol=1,symmetry=1)*circle(1),
[2,0]+set_parameters(atol=1,symmetry=8)*circle(1),
[4,0]+set_parameters(atol=1e-3)*circle(1));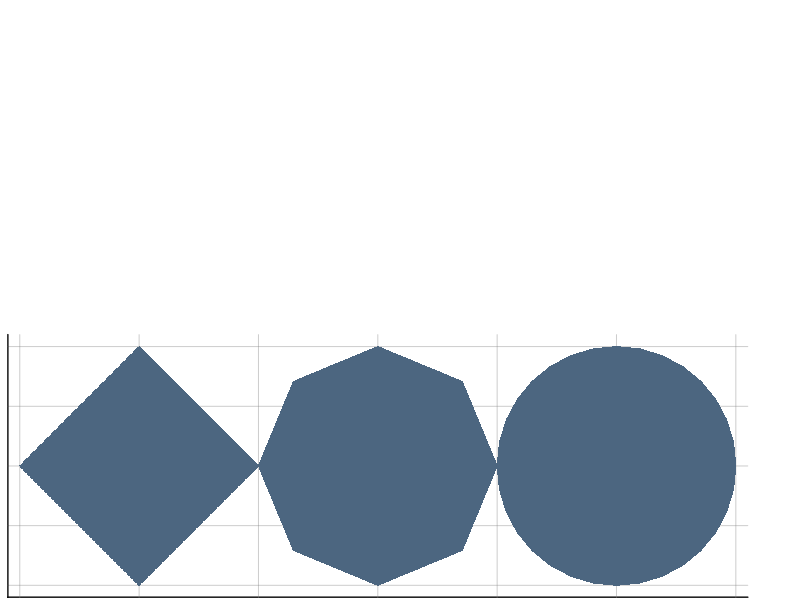
Auxiliary meshes
These are the meshes of any highlight()ed parts of the objects. Auxiliary meshes are only used for displaying (whether interactively with GLMakie, or as an image with CairoMakie); they are ignored when exporting the object to STL or SVG format.
Precision: atol and rtol
atolis the maximum absolute deviation allowed when meshing an object.
This is the maximum distance between the mesh and the ideal shape. Its dimensionality is the same as basic length units for the object (i.e. it will be understood as millimeters by most 3d slicers).
rtolis the maximum relative deviation allowed when meshing.
This is a dimensionless number.
When meshing an object, the minimum value will be used between those given by these two definitions. This means that rtol gives an absolute maximum on the number of vertices for large objects, while atol governs the number of vertices for small objects.
Default values
The default values are atol = 0.1 and rtol = 1/200. The first value means that a circle will deviate by at most 0.1mm from a perfect circle, and the latter value corresponds to the fact that large circles have 32 sides (see below).
Circles
A circle of radius $r$ is approximated by an inscribed $n$-gon. The deviation between the ideal circle and the $n$-gon is the sagitta of the circular segment with radius $r$ and central angle $2π/n$; its value is hence $s = r(1-\cos(π/n)) ≈ \frac{π^2 r}{2 n^2}$.
By definition, $\texttt{atol} = s$ while $\texttt{rtol} = s/r \approx \frac{π^2}{2 n^2}$. This gives
\[n = \min(π √{r/(2\texttt{atol})}, π/ √{\texttt{rtol})}).\]
In addition, the number of sides is bounded below to always be at least 4. The number of sides thus increases as the square root of the radius, with an upper bound. With the default parameters, one has $n ≈ \min(7√r, 32)$.
The corresponding value for OpenSCAD is $n = \min(2πr/\texttt{\textdollar fs},360/\texttt{\textdollar fa})$; with the default values $\texttt{\textdollar fa}=12$ and $\texttt{\textdollar fs=2}$, this gives $n ≈ \min(π r, 30)$.
By default, circles are meshed as regular polygons inscribed in the circle. They can also be meshed as regular polygons circumscribed to that circle, by passing the circumscribed=true parameter:
julia> s = circle(1,circumscribed=true)\circle(1);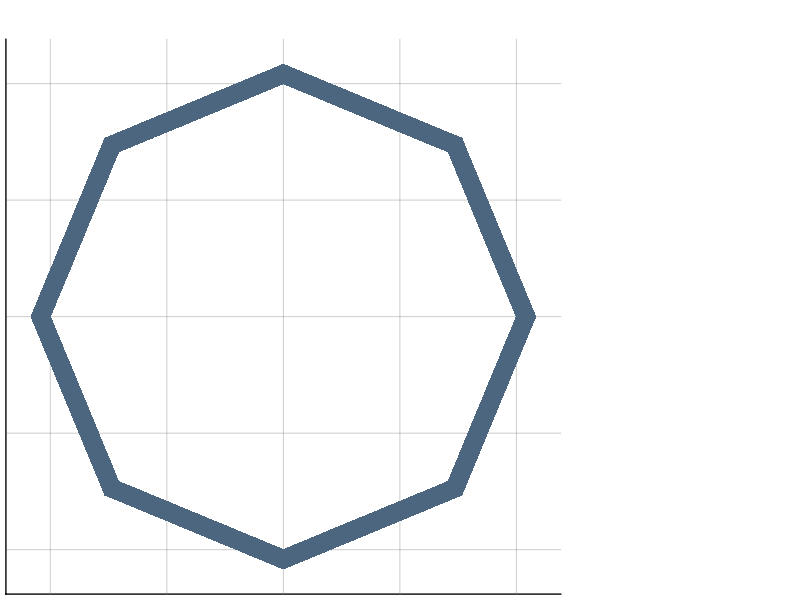 The same parameter is also available for cylinders.
The same parameter is also available for cylinders.
Spheres
Spheres are rendered as Fibonacci spheres. This produces a more regular mesh than latitude-longitude grids (in particular, the grid does not have singularities at the poles).
A sphere is approximated by an inscribed polyhedron with $n$ vertices. Such a polyhedron has $2n-4$ triangular faces; the average area of a face is $\frac{4π r^2}{2n-4} = \frac{2π r^2}{n-2}$, thus the average (squared) edge length is $d² ≈ (8π/√3) \frac{r^2}{n-2}$ (according to the unit equilateral triangle area $√3/4$).
The sagitta for a chord of length $d$ is given by $s/r = 1 - √{1-d^2/4r^2} ≈ (1-(1-d^2/8 r^2)) ≈ (π/√3)/(n-2)$. Hence we find
\[n ≈ 2 + (π/√3)/(\textrm{max}(\texttt{rtol},\texttt{atol}/r)).\]
With the default values for atol and rtol:
- small spheres have approximately $2+18r$ vertices (and always at least 6 vertices);
- large spheres have 365 vertices.
Symmetry
In addition to atol and rtol, the symmetry parameter allows forcing the number of vertices of a circle to be a multiple of a defined value (by rounding up, if needed, to a multiple of symmetry).
This parameter currently has no effect on spheres (this is on the to-do list).
Mesh types and orientation
Two-dimensional shapes
Two-dimensional objects are represented as the exclusive union (XOR) of simple-loop polygons (using even-odd rule). Internally, direct loops (counter-clockwise) represent polygons, and retrograde loops (clockwise) represent holes.
Three-dimensional volumes
Three-dimensional objects are represented as a triangle mesh, in a way compatible with LibIGL's functions. The triangles are oriented so that their normal vector points outside the volume of the object.