Transformations

All single-object transformations accept two possible syntaxes:

    transform(parameters, solid1, solid2, ...)
    transform(parameters) * solid1

The second, multiplicative form allows easy chaining of transformations:

    transform1(param1) * transform2(param2) * solid

This form may also be applied to several solids by either wrapping them in a union, or equivalently, by applying it to a Vector of such objects:

    transform(parameters) * [ solid1, solid2, ... ]

Affine transformations

ConstructiveGeometry.mult_matrix — Function
mult_matrix(a, [center=c], solid...)
mult_matrix(a, b, solid...)
mult_matrix(a, b) * solid
a * solid + b # preferred form

Represents the affine operation x -> a*x + b.

Extended help

Types of `mult_matrix` parameters

The precise type of parameters a and b is not specified. Usually, a will be a matrix and b a vector, but this is left open on purpose; for instance, a can be a scalar (for a scaling). Any types so that a * Vector + b is defined will be accepted.

Conversion to a matrix will be done when meshing.

Matrix multiplication

Chained affine transformations are composed before applying to the objects. This saves time: multiple (3 × n) matrix multiplications are replaced by (3 × 3) multiplications, followed by a single (3 × n).

julia> s = mult_matrix([1 0 0;0 1 0;0 .5 1])*cube(10);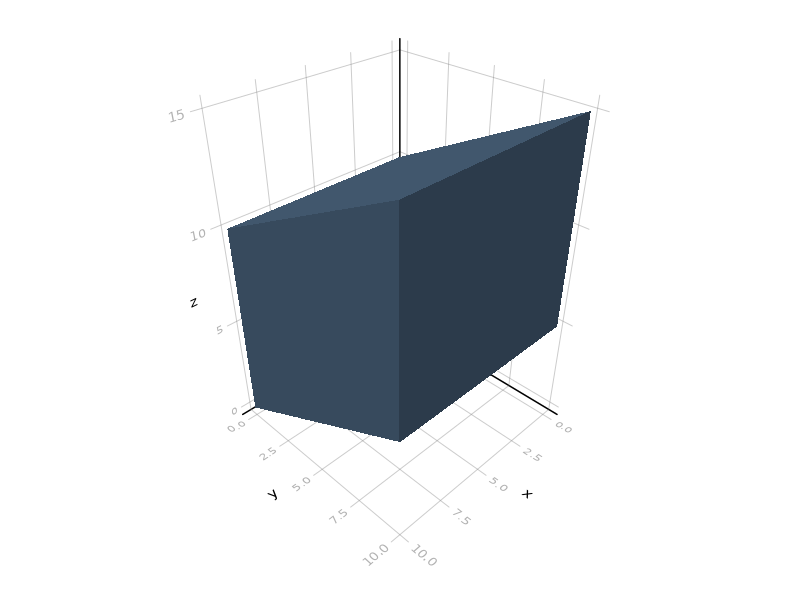

a skewed cube

Only invertible affine transformations are supported. Transformations with a negative determinant reverse the object (either reverse the polygon loops, or reverse the triangular faces of meshes) to preserve orientation.

For non-invertible transformations, see project.

Three-dimensional embeddings of two-dimensional objects

As an exception, it is allowed to apply a (2d -> 3d) transformation to any three-dimensional object. The result of such a transformation is still two-dimensional (and will accordingly be rendered as a polygon), but the information about the embedding will be used when computing convex hull or Minkowski sum with a three-dimensional object.

julia> s = hull([30,0,0]+[1 0 0;0 1 0;.5 0 0]*circle(20), [0,0,30]);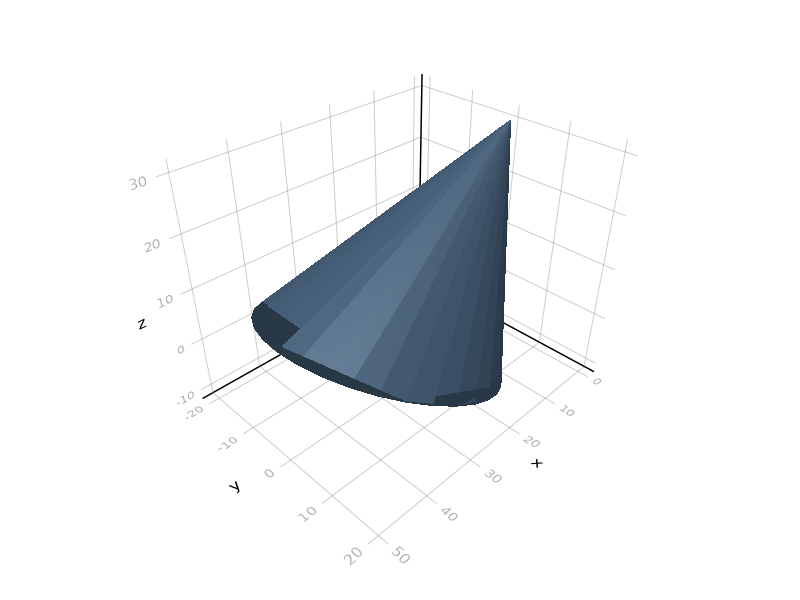

convex hull of a non-canonically embedded circle and a point

ConstructiveGeometry.scale — Function
scale(a, s...; center=0)
scale(a; center=0) * s
a * s

Scales solids s by factor a. If center is given then this will be the invariant point.

a may also be a vector, in which case coordinates will be multiplied by the associated diagonal matrix.

julia> s = [1,1.5,2]*sphere(50);

a diagonally scaled sphere produces an ellipsoid

ConstructiveGeometry.rotate — Function
rotate(θ, [center=center], [solid...])
rotate(θ, axis=axis, [center=center], [solid...])

Rotation around the Z-axis (in trigonometric direction, i.e. counter-clockwise).

rotate((θ,φ,ψ), [center=center], [solid...])

Rotation given by Euler angles (ZYX; same ordering as OpenSCAD).

Angles are in degrees by default. Angles in radians are supported through the use of Unitful.rad.

julia> s = rotate(30)*square(20);

a rotated square

ConstructiveGeometry.reflect — Function
reflect(v, s...; center=0)
reflect(v; center=0) * s

Reflection with axis given by the hyperplane normal to v. If center is given, then the affine hyperplane through this point will be used.

Overloaded operators

The following operators are overloaded.

  • matrix * solid is a linear transformation.
  • vector * solid is a multiplication by a diagonal matrix.
  • vector + solid is a translation.
  • real * solid is a scaling.
  • complex * 2dshape is a similitude.
  • color * solid is a color operation.
  • color % solid is a highlight operation.

Two-dimensional drawing

ConstructiveGeometry.offset — Function
offset(r, solid...; kwargs...)
offset(r; kwargs...) * solid

Offsets by given radius. Positive radius is outside the shape, negative radius is inside.

Parameters for 2d shapes:

ends=:round|:square|:butt|:loop
join=:round|:miter|:square
miter_limit=2.0

Parameter for 3d solids:

maxgrid = 32 # upper bound on the number of cubes used in one direction
Complexity

Offset of a volume is a costly operation; it is realized using a marching cubes algorithm on a grid defined by maxgrid. Thus, its complexity is cubic in the parameter maxgrid.

The grid size used for offsetting is derived from the atol and rtol parameters, and upper bounded by the optional maxgrid parameter (if this is different from zero).

julia> s1 = offset(10)*[square(100,50), square(50,100)];

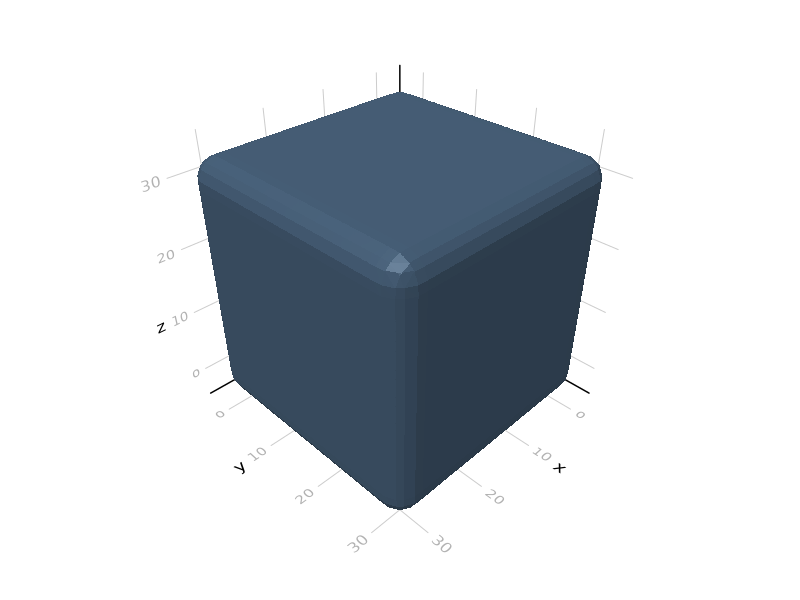
julia> s2 = offset(3)*cube(30);

example: an offset L-shapeexample: an offset cube

julia> s = opening(10)*[square(100,50), square(50,100)];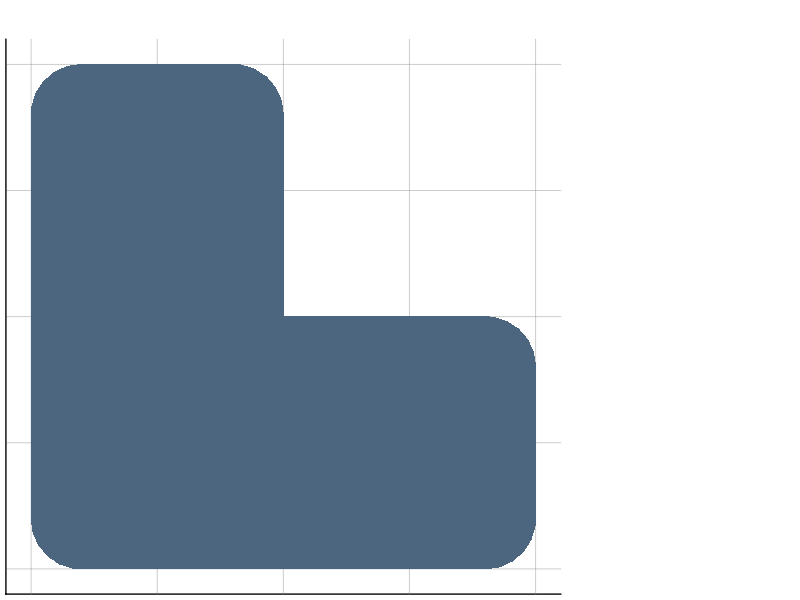

example: the opening of the L-shape

julia> s = closing(10)*[square(100,50), square(50,100)];

example: the closing of the L-shape

Extrusion

Linear extrusion

julia> s1 = linear_extrude(10)*[square(10,5), square(5,15)];


julia> s2 = linear_extrude(20, twist=45, scale=.8)*[square(10,5), square(5,15)];

example: linear extrusion of a L-shapeexample: linear extrusion with twist

ConstructiveGeometry.rotate_extrude — Function
rotate_extrude([angle = 360°], shape...; slide=0)
rotate_extrude([angle = 360°]; [slide=0]) * shape

Similar to OpenSCAD's rotate_extrude primitive.

The slide parameter is a displacement along the z direction.

julia> s1 = rotate_extrude(245)*[square(10,5), square(5,15)];


julia> s2 = rotate_extrude(720, slide=30)*translate([10,0])*square(5);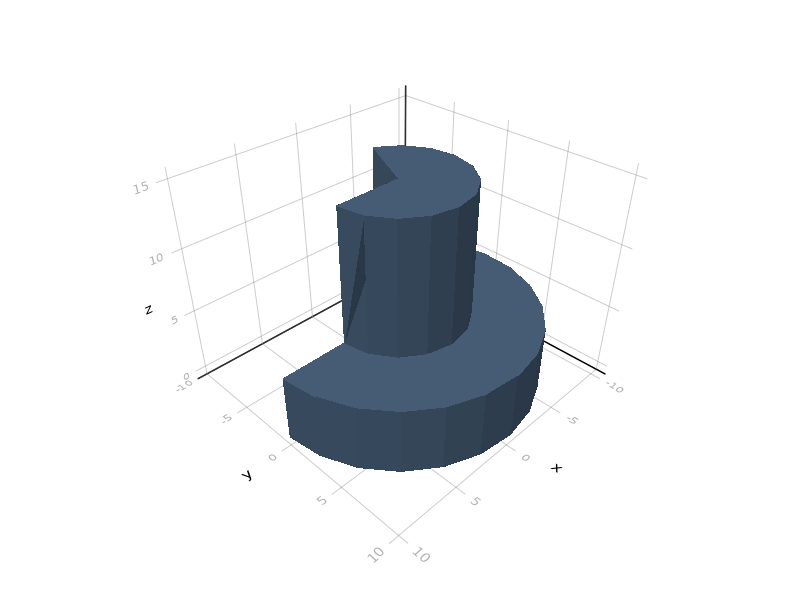

example: rotation extrusion of a L-shapeexample: rotational extrusion with slide

The cone function may also be used as an operator to build a cone out of an arbitrary shape:

julia> s = cone([1,2,3])*square(5);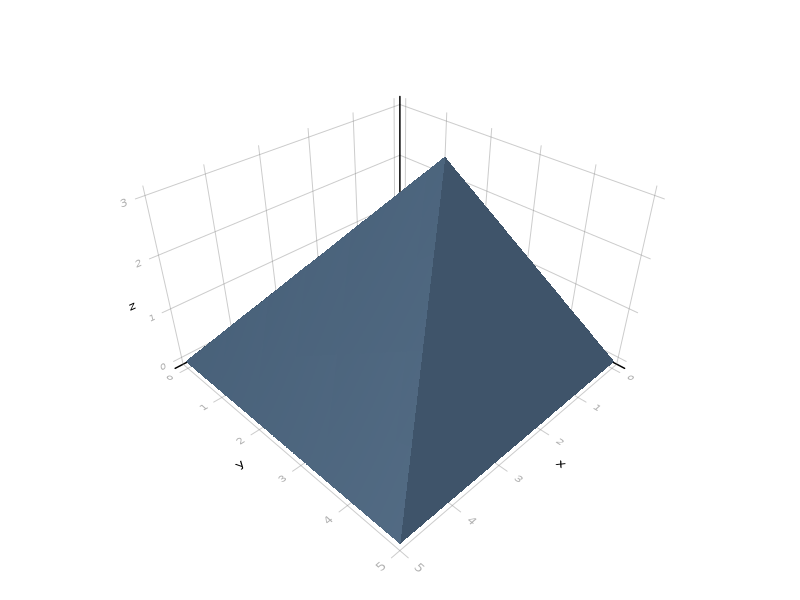

example: using cone to build a pyramid

Surface sweep

ConstructiveGeometry.sweep — Function
sweep(path, shape...)

Extrudes the given shape by

  1. rotating perpendicular to the path (rotating the unit y-vector

to the direction z), and

  1. sweeping it along the path, with the origin on the path.

FIXME: open-path extrusion is broken because ClipperLib currently does not support the etOpenSingle offset style.

A swept surface is similar to a (closed) path extrusion:

julia> s = sweep(square(50))*circle(5);

example: a circle swept along a square

Swept surfaces

A surface may only be swept along a closed loop (or the union of several closed loops) for now; this is a limitation of the clipper library, which does not support single-path extrusion for now (and this is unlikely to change in the near future).

julia> f(t) =([ cospi(t) -sinpi(t) 0;sinpi(t) cospi(t) 0;0 0 1],[0 0 10*t]);

julia> s = sweep(f; nsteps=100,maxgrid=100)*cube(20);

example: a cube swept along a helix

Decimation

These operations either reduce or increase the number of faces in a three-dimensional object.

ConstructiveGeometry.loop_subdivide — Function
loop_subdivide(n, shape...)

Applies n iterations of loop subdivision to the solid. This does not preserve shape; instead, it tends to “round out” the solid.

julia> s = loop_subdivide(4)*cube(20);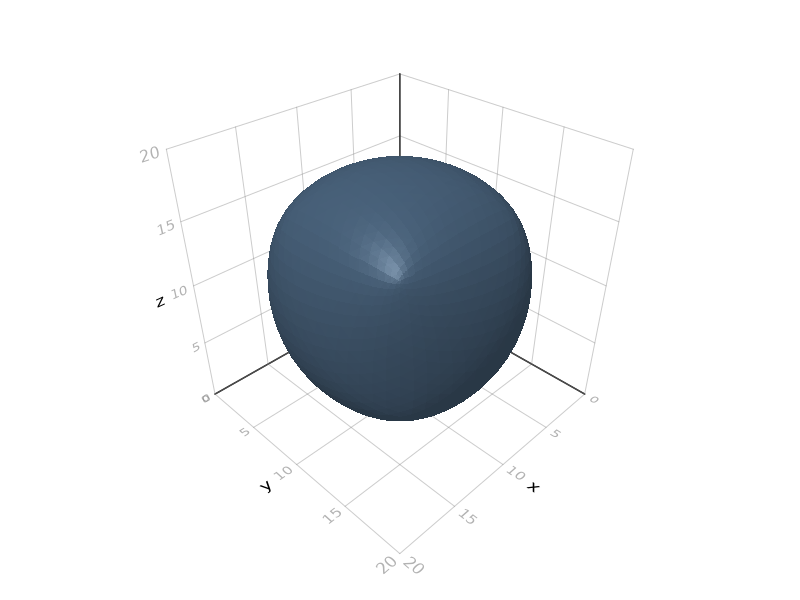

example: loop subdivision of a cube

Coloring objects

ConstructiveGeometry.color — Function
color(c::Colorant, s...)
color(c::AbstractString, s...)
color(c::AbstractString, α::Real, s...)
color(c) * s...

Colors objects s... in the given color.

julia> green, red = parse.(ConstructiveGeometry.Colorant, ("green", "red"))
(RGB{N0f8}(0.0,0.502,0.0), RGB{N0f8}(1.0,0.0,0.0))

julia> s = union(green * cube(10), [10,0,0]+red*sphere(10));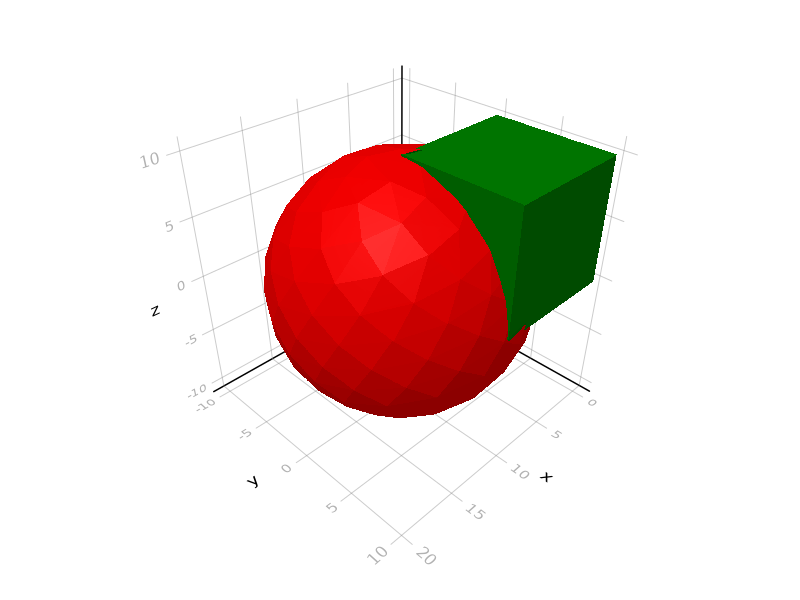

example: union of a sphere and a cube

ConstructiveGeometry.highlight — Function
highlight(c::Colorant, s)
highlight(c::AbstractString, s)
(c::Colorant) % s

Marks an object as highlighted. This means that the base object will be displayed (in the specified color) at the same time as all results of operations built from this object.

julia> s = intersect(green % cube(10), red % ([10,0,0]+sphere(10)));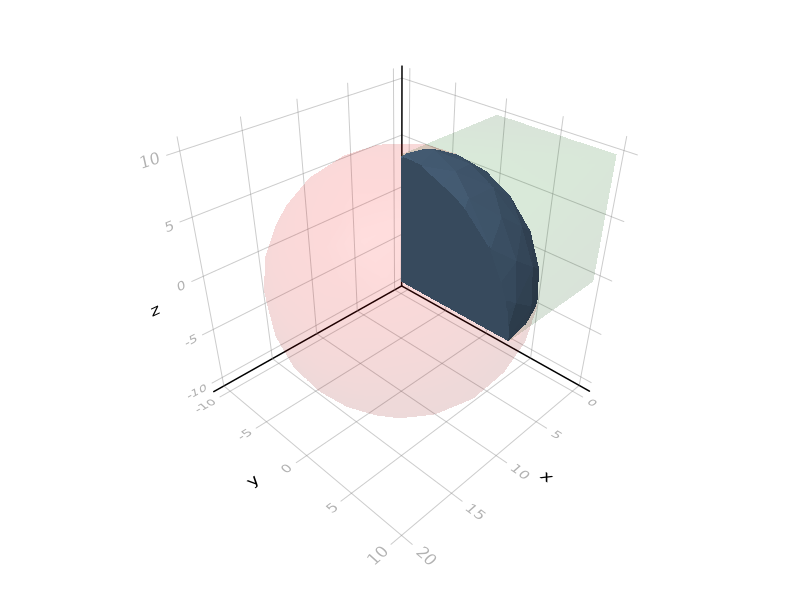

example: intersection of a highlighted sphere and a highlighted cube

Highlighted parts of objects are shown only when the object is represented as an image via the plot method (either interactively with GLMakie, or as an image with CairoMakie). For SVG and STL output, all highlighted parts are ignored.

Highlighted objects are preserved only by CSG operations and (invertible) affine transformations. For other transformations:

  • convex hull and Minkowski sum are generally increasing transformations, and would cover highlighted parts anyway;
  • projection, slicing and extrusion modify the dimension of object, making it impossible to preserve highlighted parts.

Modifying meshing parameters

ConstructiveGeometry.set_parameters — Function
set_parameters(;atol, rtol, symmetry) * solid...

A transformation which passes down the specified parameter values to its child. Roughly similar to setting $fs and $fa in OpenSCAD.

The set_parameters transformation allows attaching arbitrary metadata. This is on purpose (although there currently exists no easy way for an user to recover these metadata while meshing an object).

The values for these parameters are explained in atol and rtol.