Basic Usage
Bounding a function via McCormick operators
In order to bound a function using a McCormick relaxation, you first construct a McCormick object (x::MC) that bounds the input variables, and then you pass these variables to the desired function.
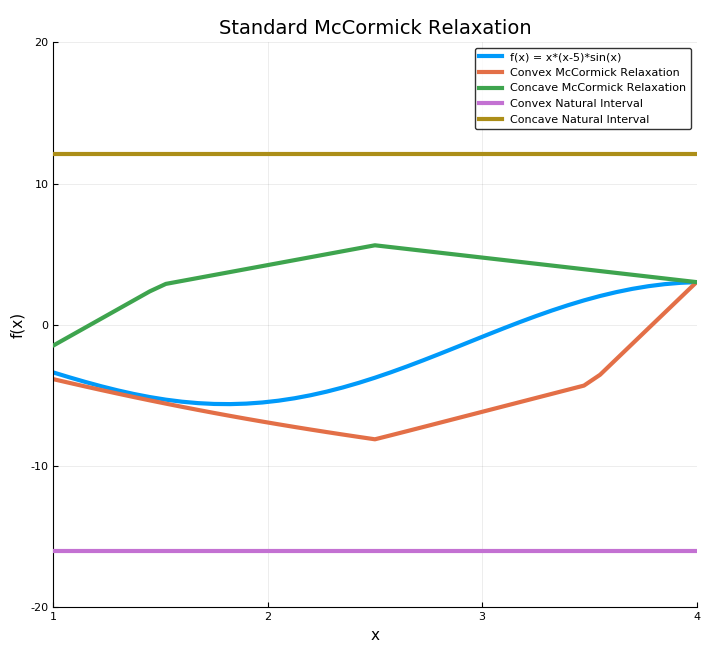
In the example below, convex/concave relaxations of the function f(x) = x * (x-5.0) * sin(x) are calculated at x = 2 on the interval [1, 4].
using EAGO, IntervalArithmetic
# Define the function we want convex/concave relaxations for
f(x) = x*(x-5.0)*sin(x)
# Create a MC object for x = 2.0 on [1.0, 4.0] to use as an
# input to f(x)
x = 2.0 # value of independent variable x
Intv = Interval(1.0,4.0) # desired interval to relax over
xMC = MC{1,NS}(x, Intv, 1) # 1-D non-smooth (NS) McCormick object,
# with a value of x and lower/upper
# bounds of Intv
fMC = f(xMC) # relax the function by passing the MC object to it
cv = fMC.cv # convex relaxation
cc = fMC.cc # concave relaxation
cvgrad = fMC.cv_grad # subgradient/gradient of convex relaxation
ccgrad = fMC.cc_grad # subgradient/gradient of concave relaxation
Iv = fMC.Intv # retrieve interval bounds of f(x) on IntvBy plotting the results we can easily visualize the convex and concave relaxations, interval bounds, and affine bounds constructed using the subgradient at the middle of X.
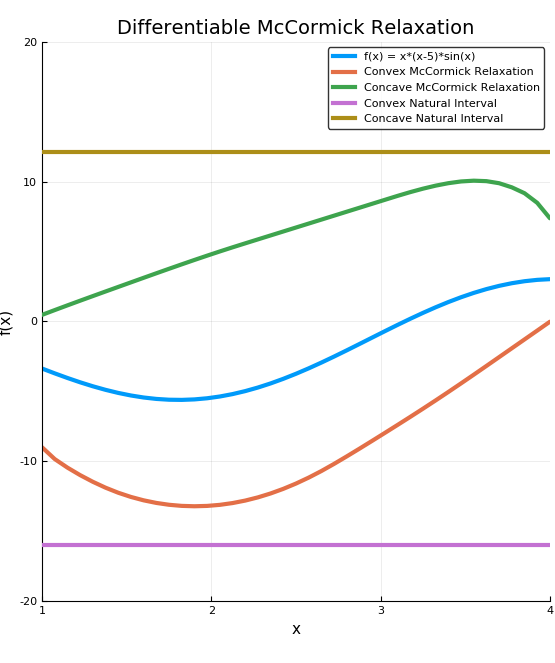
If we instead use the constructor xMC = MC{1,Diff}(x,Intv,1) in the above code and re-plot, we arrive at the following graph. Note that these relaxations are differentiable, but not as tight as the non-smooth relaxations.
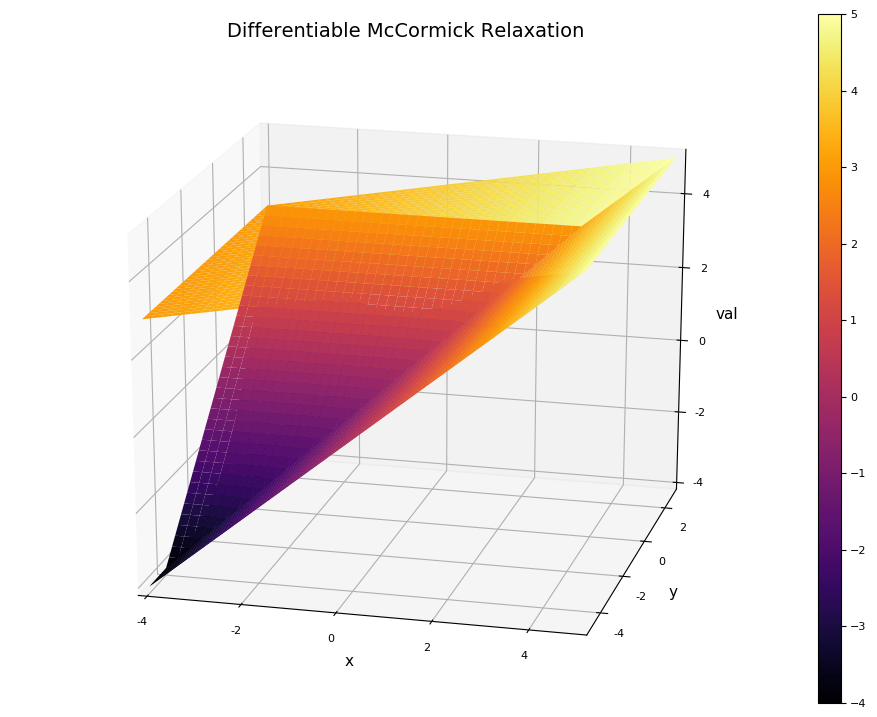
This functionality can be readily extended to multivariate functions as shown here:
f(x) = max(x[1],x[2])
x = [2.0 1.0] # values of independent variable x
Intv = [Interval(-4.0,5.0), Interval(-5.0,3.0)] # define intervals to relax over
# create McCormick object
xMC = [MC{2,Diff}(x[i], Intv[i], i) for i=1:2)]
fMC = f(xMC) # relax the function
cv = fMC.cv # convex relaxation
cc = fMC.cc # concave relaxation
cvgrad = fMC.cv_grad # subgradient/gradient of convex relaxation
ccgrad = fMC.cc_grad # subgradient/gradient of concave relaxation
Iv = fMC.Intv # retrieve interval bounds of f(x) on Intv