Documentation
Requirements & Installation
Julia: version ≥ 1.2
Packages: see the dependencies of the main module.
To install the package execute the following command in Julia's REPL:
]add CovarianceEstimation PosDefManifold DiagonalizationsQuick Start
Copy and execute the examples .jl units provided in the examples folder or walk throught the documentation and run the examples you will find there.
Disclaimer
This version is throughoutly tested for both the case of real and complex data input. Independent reviewers for both the code and the documentation are welcome.
TroubleShoothing
| Problem | Solution |
|---|---|
| No problem has been reported so far |
About the Authors
Marco Congedo, corresponding author, is a Research Director of CNRS (Centre National de la Recherche Scientifique), working at UGA (University of Grenoble Alpes). Contact: first name dot last name at gmail dot com
Overview
Diagonalizations.jl implements the following multivariate linear filters:
Table 1
| Acronym | Full Name | Datasets ( m ) | Observations ( k ) |
|---|---|---|---|
| PCA | Principal Component Analysis | 1 | 1 |
| Whitening | Whitening (Sphering) | 1 | 1 |
| MCA | Maximum Covariance Analysis | 2 | 1 |
| CCA | Canonical Correlation Analysis | 2 | 1 |
| gMCA | generalized MCA | >1 | 1 |
| gCCA | generalized CCA | >1 | 1 |
| CSP | Common Spatial Pattern | 1 | 2 |
| CSTP | Common Spatio-Temporal Pattern | 1 | >1 |
| AJD | Approximate Joint Diagonalization | 1 | >1 |
| mAJD | multiple AJD | >1 | >1 |
All these filters are obtained by diagonalization procedures and can be all understood as particular solutions to the same optimization problem, which corresponds to the mAJD problem. (Congedo, 2013 🎓). They can be classified in several way. For instance,
- the MCA can be seen as a bilinear version and the gMCA as a multi-linear version of the PCA.
- the CCA can be seen as a bilinear version and the gMCA as a multi-linear version of Whitening.
- the AJD can be seen as a generalization of the PCA and of the CSP.
- the mAJD can be seen as a generalization of all other filters.
Also,
- PCA and Whitening are based on the eigenvalues decomposition
- MCA and PCA are based on the singular values decomposition
- CSP and CSTP are based on the generalized eigenvalue decomposition.
- gMCA, gCCA, AJD and mAJD are solved by iterative algorithms generalizing the above well-known procedures.
With respect to the number of datasets ( m ) and observations ( k ) the implemented filters fill the entries of the following table:
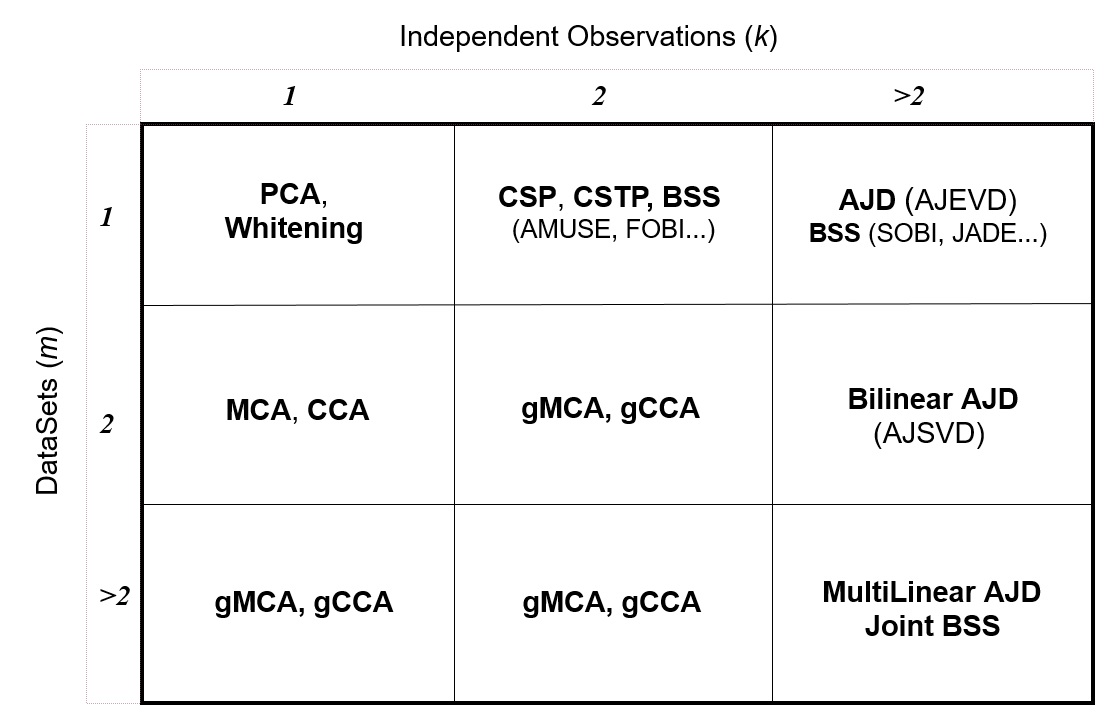
Figure 1Taxonomy of several diagonalization procedures and signal procssing methods that make use of them, depending on the number of observations and data sets involved. Legend: see acronyms.
Future versions shall concentrate on implementing other iterative algorithms for solving the generalized problems. Also, this package will be used as the base of packages implementing practical signal processing methods such as blind source separation.
As compared to MultivariateStats.jl this package supports :
- the
dimskeyword - shrinkage covariance matrix estimations throught package CovarianceEstimation
- average covariance estimations with metrics for the manifold of positive definite matrices using the PosDefManifold package
- automatic procedures to set the subspace dimension
- diagonalization procedures for the case $m≥2$ and $k≥2$ (see Fig. 1).
Code units
Diagonalizations.jl includes twelve code units (.jl files):
| Unit | Description |
|---|---|
| Diagonalizations.jl | Main module, declaring constants, types and structs |
| pca.jl | Unit implementing the PCA and the Whitening |
| cca.jl | Unit implementing the MCA and the CCA |
| gcca.jl | Unit implementing the gMCA and the gCCA |
| csp.jl | Unit implementing the CSP and CSTP |
| ajd.jl | Unit implementing the AJD and the mAJD |
| tools.jl | Unit containing general tools and internal functions |
| Gajd.jl | Unit implementing the GAJD and GLogLike iterative algorithms (in the 'optim' folder) |
| Jade.jl | Unit implementing the JADE and JADEmax iterative algorithms (in the 'optim' folder) |
| JoB.jl | Unit implementing the OJoB and NoJoB iterative algorithms (in the 'optim' folder) |
| LogLike.jl | Unit implementing the Log-Likelihood iterative algorithms (in the 'optim' folder) |
| QnLogLike.jl | Unit implementing the quasi-Newton Log-Likelihood iterative algorithm (in the 'optim' folder) |
Furthermore, all examples given at the end of the documentation of the filter constructors are collected as .jl units in the 'examples' folder.
🎓
References
P. Ablin, J.F. Cardoso, A. Gramfort (2019) Beyond Pham's algorithm for joint diagonalization, Proc. ESANN Conference.
A. Belouchrani, K. Abed-Meraim, J. Cardoso, E. Moulines (1997), A blind source separation technique using second order statistics, IEEE Transactions on Signal Processing, 45(2), 434–444.
J.-F. Cardoso (1989) Source separation using higher order moments. In Proc. IEEE ICASSP, 4, 2109-2112
J.-F. Cardoso and A. Souloumiac (1993) Blind beamforming for non gaussian signals. In IEE Proceedings-F, 140, 362–370.
J.-F. Cardoso, A. Souloumiac (1996) Jacobi angles for simultaneous diagonalization. SIAM Journal on Matrix Analysis and Applications, 17(1), 161–164.
M. Congedo (2013) EEG Source Analysis Thesis submitted in partial fulfillment of the requirements to obtain the H.D.R degree presented at doctoral school EDISCE, University of Grenoble Alpes, France.
M. Congedo M, A. Barachant A, R. Bhatia (2017) Riemannian Geometry for EEG-based Brain-Computer Interfaces; a Primer and a Review, Brain-Computer Interfaces, 4(3), 155-174.
M. Congedo, C. Gouy-Pailler, C. Jutten (2008) On the blind source separation of human electroencephalogram by approximate joint diagonalization of second order statistics. Clinical Neurophysiology 119, 2677-2686.
M. Congedo, L. Korczowski, A. Delorme, F. Lopes Da Silva (2016) Spatio-Temporal Common Pattern; a Companion Method for ERP Analysis in the Time Domain, Journal of Neuroscience Methods, 267, 74-88.
M. Congedo, R. Phlypo, J. Chatel-Goldman (2012) Orthogonal and Non-Orthogonal Joint Blind Source Separation in the Least-Squares Sense, 20th European Signal Processing Conference (EUSIPCO), 1885-9.
M. Congedo, R. Phlypo, D.-T. Pham (2011) Approximate joint singular value decomposition of an asymmetric rectangular matrix set, IEEE Trans Signal Process, 59(1), 415-424.
B.N. Flury, W. Gautschi (1986) An algorithm for the simultaneous orthogonal transformation of several positive de finite symmetric matrices to nearly orthogonal form. Siam J. of Sci. Stat. Comp., 7(1), 169-184.
K. Fukunaga (1990) Introduction to Statistical Pattern Recognition (2nd Ed.), Academic Press, London.
I.J. Good (1969) Some Applications of the Singular Decomposition of a Matrix. Technometrics, 11(4), 823-831.
H. Hotelling (1936) Relations between two sets of variates. Biometrika, 27, 321-77.
O. Ledoit, M. Wolf (2004) A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices, Journal of Multivariate Analysis, 88(2), 365-411.
O. Ledoit, M. Wolf (2018) Analytical Nonlinear Shrinkage of Large-Dimensional Covariance Matrices, Working Paper No. 264, University of Zurich.
L Molgedey, H.G. Schuster (1994) Separation of a Mixture of Independent Signals using Time Delayed Correlations. Physical Review Letters, 72, 3634-3636.
K. Pearson (1901) On Lines and Planes of Closest Fit to Systems of Points in Space. Philosophical Magazine, 2(11), 559–572.
D.-T. Pham (2000) Joint approximate diagonalization of positive definite matrices, SIAM Journal on Matrix Analysis and Applications, 22(4), 1136–1152.
J.R. Schott (1997) Matrix Analysis for statistics, John Wiley & Sons, New York.
P. Tichavsky, A. Yeredor (2009), Fast approximate joint diagonalization incorporating weight matrices, IEEE Trans. Signal Process., 57(3), 878–891. https://staff.utia.cas.cz/files/Soutez_09/Tichavsky/WEDGE09.pdf
L. Tong, V. Soon, Y. Huang, R.W. Liu (1991), A necessary and sufficient condition Waveform-Preserving Blind Estimation of Multiple Independent Sources. IEEE Transactions on Signal Processing, 41(7), 2461-2470.
K. Usevich, J. Li, P. Comon (2020), Approximate matrix and tensor diagonalization by unitary transformations: convergence of Jacobi-type algorithms, preprint: hal-01998900v3f.