Droop Mode - Simple Grid Forming
| Mode | Description | |
|---|---|---|
| 1 | "Swing" | Ideal voltage source without dynamics (i.e., an infinite bus) |
| 2 | "PQ" | Grid following controllable source/load (real and imaginary power) |
| 3 | "Droop" | Simple grid forming with power balancing through a droop mechanism |
| 4 | "Synchronverter" or "VSG" | Grid forming control mimicking a generator, i.e., virtual synchronous generator |
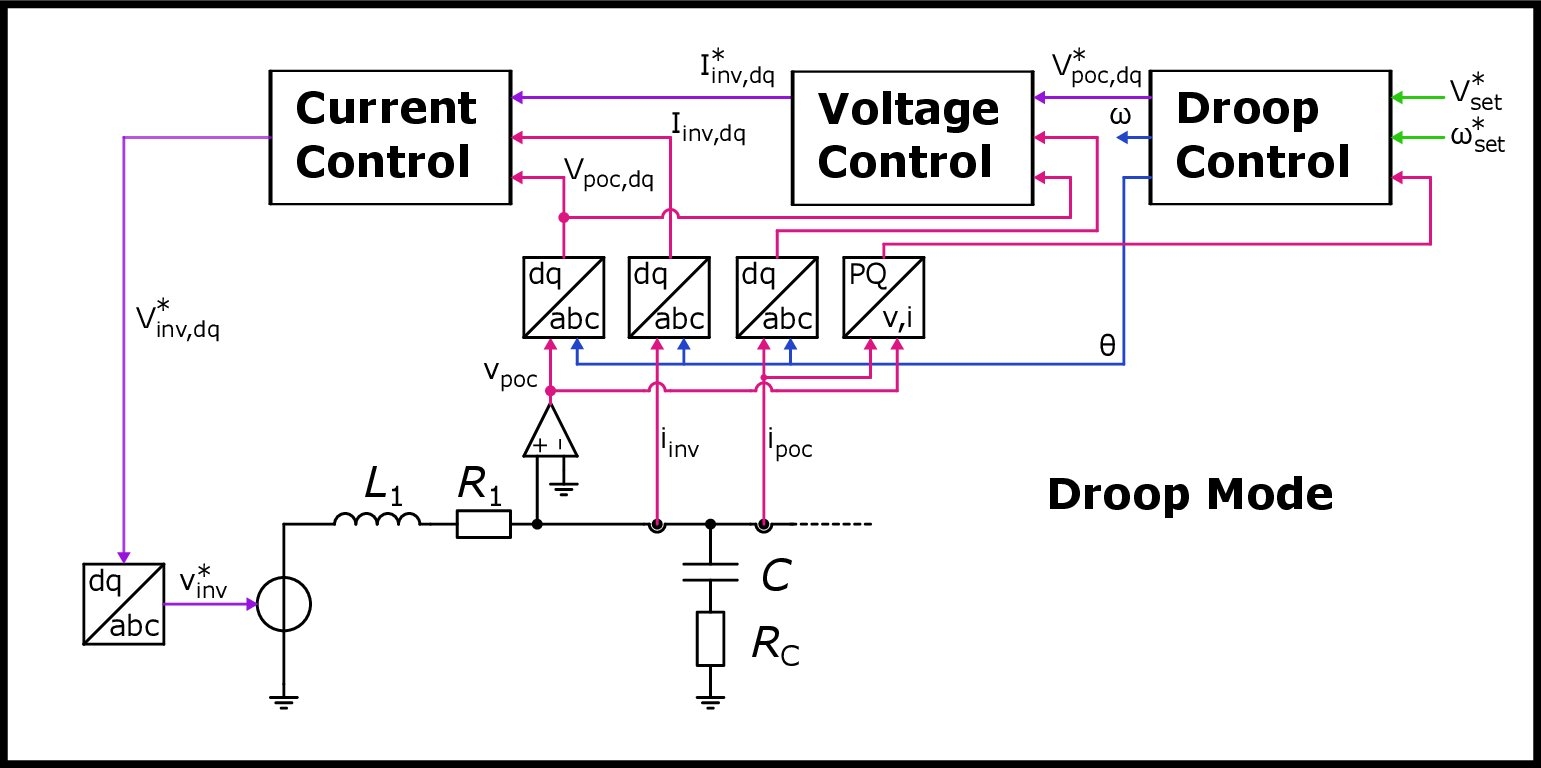
- The control structure of power electronic inverters can be divided into cascading levels.
- The second level above the current control loop is a voltage control loop.
- A third level on top of the voltage control is called "Droop".
Summary
- The following example is intended to introduce you to a decentralised and self-organising control mode.
- The mode "communicates" with other inverters in the network through the voltage and frequency.
- Often battery energy storage systems (BESSs) operate in this mode, especially in remote islanded grid areas.
- This mode is autonomous and provides a measure of "inertia" to the network.
Theory
The droop control method can be referred to as an independent, autonomous concept since intercommunication links between the converters other than the electrical cables can be eliminated. That is, in a network with loads and inverters in droop mode, the power required by the loads is partitioned amongst the inverters in droop modes by only varying electrical quantities are their respective control points.
This mode works quite well when high frequency harmonics and switching ripples are neglected (as they presently are in the set-up). An inverter in "Droop" mode is capable of other negative oscillatory behaviour, similar to the hunting effect in synchronous generators. In fact, the droop mode is a simplified version of the Virtual Synchronous Generator (VSG) mode with a low-pass filtering characteristic on the measured real and imaginary powers. Unlike the PQ mode, a source in droop mode has to have some energy storage available.
The voltage control loop has a very similar structure to the inner current control loop, also operating in the DQ0 frame and with PI controllers. 
The "droop" control sitting on top of the voltage control loop, provides the reference voltage signals. The droop mode for every inverter has two coefficients, $D_p$ and $D_q$, that determine its behaviour. $D_p$ is associated with the real power and frequency, while $D_q$ corresponds to the voltage magnitude and the imaginary power. These coefficients can by tuned either heuristically or via more advanced optimisation algorithms.

If the user does not specify $D_p$ and $D_q$, then they are automatically tuned based on the converter power rating and the network's maximum allowable frequency and voltage deviations, i.e., $Δfmax$ and $ΔEmax$. The formulas that are implemented to calculate the droop coefficients are as follows,
\[ D_p = \frac{S_{rated}}{{ω_{set}}^2 Δfmax}, \quad D_q = \frac{S_{rated}}{V_{set}*\sqrt{2}*ΔEmax}.\]
using ElectricGrid;_______________________________________________________________________________
Network Configuration
- Two inverters are connected to each other through a cable.
- The one inverter is placed in the familiar PQ mode, while the other is in droop mode.
- The droop inverter will regulate the frequency and the PQ inverter will follow along.
- If not provided by the user, the proportional and integral gains for the PI controllers are tuned automatically via a loop-shaping method.
With this configuration, a time domain simulation is conducted below.
# total run time, seconds
t_end = 0.08
# Connectivity Matrix
CM = [ 0. 1.
-1. 0.]
parameters = Dict{Any, Any}(
"source" => Any[
Dict{Any, Any}("pwr" => 400e3, # Rated appared power [VA]
"mode" => "Droop", # Controller mode
"V_kp" => 0.6, # Voltage proportional gain [A/V] (**optional**)
"V_ki" => 12, # Current integral gain [A/V⋅s] (**optional**)
"Dp" => 810, # Frequency droop coefficient [N⋅m⋅s/rad] (**optional**)
"Dq" => 24e3) # Voltage droop coefficient [VAi/V] (**optional**)
Dict{Any, Any}("pwr" => 100e3,
"mode" => "PQ",
"p_set" => 50e3, # Real power set point (generating) [W]
"q_set" => -40e3) # Imaginary power set point (inductive) [VAi]
],
"cable" => Any[
Dict{Any, Any}("R" => 0.1,
"L" => 0.25e-3,
"C" => 0.1e-4),
],
"grid" => Dict{Any, Any}("Δfmax" => 0.5, # The % drop (increase) in frequency that causes a 100% increase (decrease) in active power (from nominal).
"ΔEmax" => 5) # The % drop (increase) in voltage that causes a 100% increase (decrease) in reactive power (from nominal).
);
env = ElectricGridEnv(CM = CM, parameters = parameters, t_end = t_end, verbosity = 2);
agents = SetupAgents(env);
hook = Simulate(agents, env);┌ Info: Normalization is done based on the defined parameter limits.
└ @ JEG c:\Gitlab\JEG\ElectricGrid.jl\src\electric_grid_env.jl:329
┌ Info: Time simulation run time: 0.08 [s] ~> 801 steps
└ @ JEG c:\Gitlab\JEG\ElectricGrid.jl\src\electric_grid_env.jl:330
┌ Info: 2 'classically' controlled sources have been initialised.
└ @ JEG c:\Gitlab\JEG\ElectricGrid.jl\src\classical_control.jl:2686
┌ Info: 1 source has been set up in PQ mode.
└ @ JEG c:\Gitlab\JEG\ElectricGrid.jl\src\classical_control.jl:2695
┌ Info: 1 source has been set up in Droop mode.
└ @ JEG c:\Gitlab\JEG\ElectricGrid.jl\src\classical_control.jl:2695
┌ Info: 2 sources have automatically calculated proportional and integral gains for their current control loops.
└ @ JEG c:\Gitlab\JEG\ElectricGrid.jl\src\classical_control.jl:2720_______________________________________________________________________________
Low-Level Rendering
RenderHookResults(hook = hook,
states_to_plot = ["source1_i_L1_a"], # Inductor current [A]
actions_to_plot = ["source1_u_a"], # Inverter voltage [V]
)_______________________________________________________________________________
High-Level Rendering
RenderHookResults(hook = hook,
states_to_plot = [],
actions_to_plot = [],
v_mag_poc = [1], # Scaled L₂ norm in αβγ coordinates [V]
power_p_inv = [2], # Real power [Watts]
power_q_inv = [2], # Imaginary power [VAi]
power_p_poc = [1], # Real power [Watts]
power_q_poc = [1], # Imaginary power [VAi]
angles = [1 2], # Relative angle [degrees]
freq = [1 2], # Angular velocity [Hz]
)_______________________________________________________________________________
Analysis
- As expected, the inverter in PQ mode behaves in a grid-following manner.
- Notice that the frequency of the network is not exactly 50 Hz. This is due to the frequency droop mechanism.
- Neither does the voltage magnitude in steady state equal 230 V. This is due to the voltage droop mechanism.
_______________________________________________________________________________
References
- N. Pogaku, M. Prodanovic and T. C. Green, "Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid," in IEEE Transactions on Power Electronics, vol. 22, no. 2, pp. 613-625, March 2007, doi: 10.1109/TPEL.2006.890003.
- J. M. Guerrero, J. C. Vasquez, J. Matas, L. G. de Vicuna and M. Castilla, "Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization," in IEEE Transactions on Industrial Electronics, vol. 58, no. 1, pp. 158-172, Jan. 2011, doi: 10.1109/TIE.2010.2066534.