Train an RL agent interacting with a stable grid
This section will show how combine classic stat-of-the-art controllers with reinforcement learning (RL) agents. As example will show how to control one source with an RL agent learning a control task while connected to a stable grid provided by a classic controller. The topics covered are:
Merging classic controllers and RL agents,
Reward and featurize functions with named policys,
MultiController,
Training an RL agent in a classicly controlled grid.
The interactive content related to the section described here can be found in the form of a notebook here.
Merging classic controllers and RL agents
In the following the RL agent is trained to draw current from a stable grid. The 3-phase electric power grid is formed by a classic controller in open-loop (Swing) mode. For more details about how the classic control works, see Classical_Controllers_Introduction.ipynb.
The use case is shown in the figure below. This environment consists of a 3-phase electrical power grid with 2 sources connected via a cable (for improved clarity, only one phase is shown in the following figure).
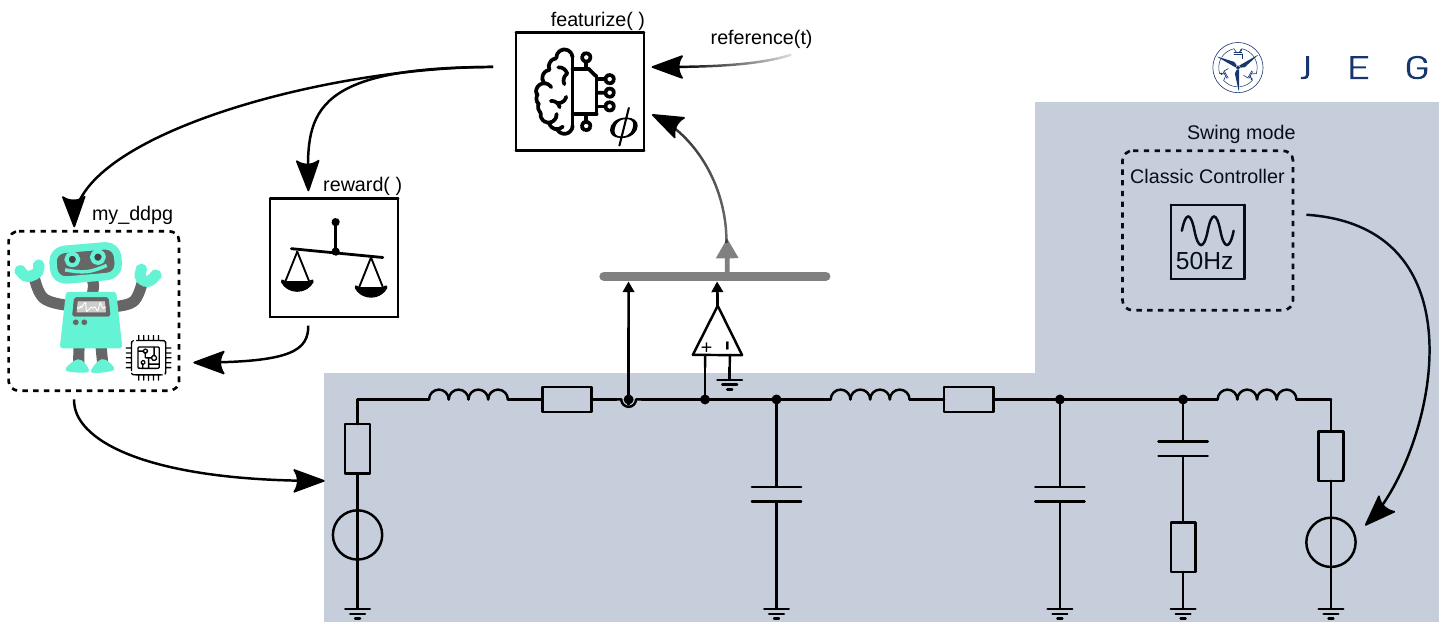
The first source is controlled by the RL agent my_ddpg which should learn to draw power from the grid, therefore act like an active load. The second source is controlled by a classic controller in open-loop mode. The swing mode is used to create a stable 3-phase grid to supply the load.
The environment is configured like described in Configuring the Environment using the parameter dict:
using ElectricGrid
parameters =
Dict{Any, Any}(
"source" => Any[
Dict{Any, Any}(
"pwr" => 200e3,
"control_type" => "RL",
"mode" => "my_ddpg",
"fltr" => "L"),
Dict{Any, Any}(
"pwr" => 200e3,
"fltr" => "LC",
"control_type" =>
"classic", "mode" => 1),
],
"grid" => Dict{Any, Any}(
"phase" => 3,
"ramp_end" => 0.04,)
)An appropriate reference(t) function has to be defined to represent the control objectives. In this example, the time t will be handed over to the function to generate time-varying reference signals. In more detail a three-phase sinusoidal reference signal shifted by 120° and an amplitude of 10 A is created. This should teach the agent to draw time-varying current from the grid. The phase is thereby chosen similar to the definition in the Swing mode:
\[i_\mathrm{L,ref} = - 10 \,\text{cos}\left(2 \pi \,50 \, t - \frac{2}{3} \pi (n-1) \right)\]
, with $n \in [0,1,2]$.
Here, $n$ represents the index refering to the 3 phases of the grid.
For more enhanced reference functions, the reference current could be chosen with regards to power (active and reactive) reference values. Feel free to implement, change and contribute!
function reference(t)
θ = 2*pi*50*t
θph = [θ; θ - 120π/180; θ + 120π/180]
return -10 * cos.(θph)
endReward and featurize functions with named policies
Afterwards the featurize() function adds the signal generated by the reference function to the state for the agent my_ddpg:
featurize_ddpg = function(state, env, name)
if name == "my_ddpg"
norm_ref = env.nc.parameters["source"][1]["i_limit"]
state = vcat(state, reference(env.t)/norm_ref)
end
endThen, the reward() function is defined. Here, again it is based on the root-mean square error (RMSE) teaching the agent my_ddpg to match the reference signal to the measured signal.
If the measured state is greater than 1 a punishment is returned which is chosen to be r = -1. It not and if the measured value differs from the reference, the average error is substracted from the maximal reward: r = 1 - RMSE:
\[r = 1 - \frac{1}{3} \sum_{{p \in \{\mathrm{a,b,c}\}}} \sqrt{\frac{|i_\mathrm{L,ref,p} - i_\mathrm{L1,p}|}{2}}\]
This function is only used if the name of the policy is my_ddpg which was chosen in the parameter dict. In any other case, 1 is returned. This could be used to define 2 different reward functions for 2 different agents via name (e.g., my_ddpg and my_sac) to learn for example a current control with the my_ddpg agent but a voltage control task with the my_sac agent.
Here, in any case but name == my_ddpg - so in case of the classic controller r = 1 is returned.
function reward_function(env, name = nothing)
if name == "my_ddpg"
state_to_control_1 = env.state[findfirst(x -> x == "source1_i_L1_a", env.state_ids)]
state_to_control_2 = env.state[findfirst(x -> x == "source1_i_L1_b", env.state_ids)]
state_to_control_3 = env.state[findfirst(x -> x == "source1_i_L1_c", env.state_ids)]
state_to_control = [state_to_control_1, state_to_control_2, state_to_control_3]
if any(abs.(state_to_control).>1)
return -1
else
refs = reference(env.t)
norm_ref = env.nc.parameters["source"][1]["i_limit"]
r = 1-1/3*(sum((abs.(refs/norm_ref - state_to_control)/2).^0.5))
return r
end
else
return 1
end
endThen, the defined parameters, featurize and reward functions are used to create an environment consisting of the electircal power grid. Here, no CM matrix defining the connection is used. Since the grid consists only of 2 sources that is the only connection possible. The ElectricGridEnv creates this internally based on the length of the parameter dict sources.
env = ElectricGridEnv(
parameters = parameters,
t_end = 0.1,
featurize = featurize_ddpg,
reward_function = reward_function,
action_delay = 0);MultiController
The MultiController ensured that the correct states and actions are linked to the corresponding controllers/agents based on the "control_type" and "mode" defined in the parameter dict.
"control_type" = "classic": Predefined classic controllers are used to calculate the actions for that source based on its states."control_type" = "RL": Based on the defined agent name (here,my_ddpg), the corresponding states are forwarded to the defined RL agent which returns the actions beloning to the source.
In the following, we will use the CreateAgentDDPG() methode to create the DDPG agent. This agent is linked in the my_custom_agents dict to the chosen name my_ddpg, which is used in the SetupAgents method to configure the control side of the experiment:
agent = CreateAgentDdpg(na = length(env.agent_dict["my_ddpg"]["action_ids"]),
ns = length(state(env, "my_ddpg")),
use_gpu = false)
my_custom_agents = Dict("my_ddpg" => agent)
controllers = SetupAgents(env, my_custom_agents);Like shown in the following figure, the controllers struct consists of 2 agents now - one per source.

Since 2 sources are defined in the env here, one controlled classically and the other by RL, the MultiController hands over the correct indices of the environment to the controllers. This enables each controller, e.g., to find the correct subset of states in the entire environment state set. In the parameter dict the first source is labeled to be controlled by the RL agent we named my_ddpg:
controllers.agents["my_ddpg"]Dict{Any, Any} with 3 entries:
"policy" => typename(Agent)…
"action_ids" => ["source1_u_a", "source1_u_b", "source1_u_c"]
"state_ids" => ["source1_i_L1_a", "source1_v_C_cables_a", "source1_i_L1_b", …Like introduced, it has knowledge about the state and action indices of the first source.
The second source is controlled via the classic controller:
controllers.agents["classic"]Dict{Any, Any} with 3 entries:
"policy" => typename(NamedPolicy)…
"action_ids" => ["source2_u_a", "source2_u_b", "source2_u_c"]
"state_ids" => ["source2_i_L1_a", "source2_v_C_filt_a", "source2_v_C_cables_…Training an RL agent in a classicly controlled grid
Then the Learn() function can be used to train the agent. Here, only the RL agent is trained. The classic controller is executed to control the second source without parameter adaptions. The Simulate() function can be used to run a test episode without action noise.
hook_learn = Learn(controller, env, num_episodes = 1000);
hook_sim = Simulate(controller, env, hook=hook);