Mixed Finite Element Methods for Poisson's Equation
In this section, we consider solving the Poisson's equation using mixed finite element methods
with boundary conditions
We reformulate the Eq. 1 as
The mixed variational formulation is to find $(\sigma, u)\in H(\text{div}, \Omega) \times L^2(\Omega)$, such that
We use the following stable pair of elements: BDM${}_1$-P${}_0$, where the stress space is approximated using a BDM element while the displacement space is approximated using a piecewise constant element.
The code is as follows:
# Solves the Poisson equation using the Mixed finite element method
using Revise
using AdFem
using DelimitedFiles
using SparseArrays
using PyPlot
n = 50
mmesh = Mesh(n, n, 1/n, degree = BDM1)
testCase = [
((x, y)->begin
x * (1-x) * y * (1-y)
end,
(x, y)->begin
-2x*(1-x) -2y*(1-y)
end), # test case 1
((x, y)->begin
x^2 * (1-x) * y * (1-y)^2
end,
(x, y)->begin
2*x^2*y*(1 - x) + 2*x^2*(1 - x)*(2*y - 2) - 4*x*y*(1 - y)^2 + 2*y*(1 - x)*(1 - y)^2
end) ,# test case 2
(
(x, y)->x*y,
(x, y)->0.0
), # test case 3
(
(x, y)->x^2 * y^2 + 1/(1+x^2),
(x, y)->2*x^2 + 8*x^2/(x^2 + 1)^3 + 2*y^2 - 2/(x^2 + 1)^2
), # test case 4
]
for k = 1:4
@info "TestCase $k..."
ufunc, ffunc = testCase[k]
A = compute_fem_bdm_mass_matrix1(mmesh)
B = compute_fem_bdm_div_matrix1(mmesh)
C = [A -B'
-B spzeros(mmesh.nelem, mmesh.nelem)]
gD = bcedge(mmesh)
t1 = eval_f_on_boundary_edge(ufunc, gD, mmesh)
g = compute_fem_traction_term1(t1, gD, mmesh)
t2 = eval_f_on_gauss_pts(ffunc, mmesh)
f = compute_fvm_source_term(t2, mmesh)
rhs = [-g; f]
sol = C\rhs
u = sol[mmesh.ndof+1:end]
close("all")
figure(figsize=(15, 5))
subplot(131)
title("Reference")
xy = fvm_nodes(mmesh)
x, y = xy[:,1], xy[:,2]
uf = ufunc.(x, y)
visualize_scalar_on_fvm_points(uf, mmesh)
subplot(132)
title("Numerical")
visualize_scalar_on_fvm_points(u, mmesh)
subplot(133)
title("Absolute Error")
visualize_scalar_on_fvm_points( abs.(u - uf) , mmesh)
savefig("bdm$k.png")
endHere we have 4 test cases, and we show the results for each test case:
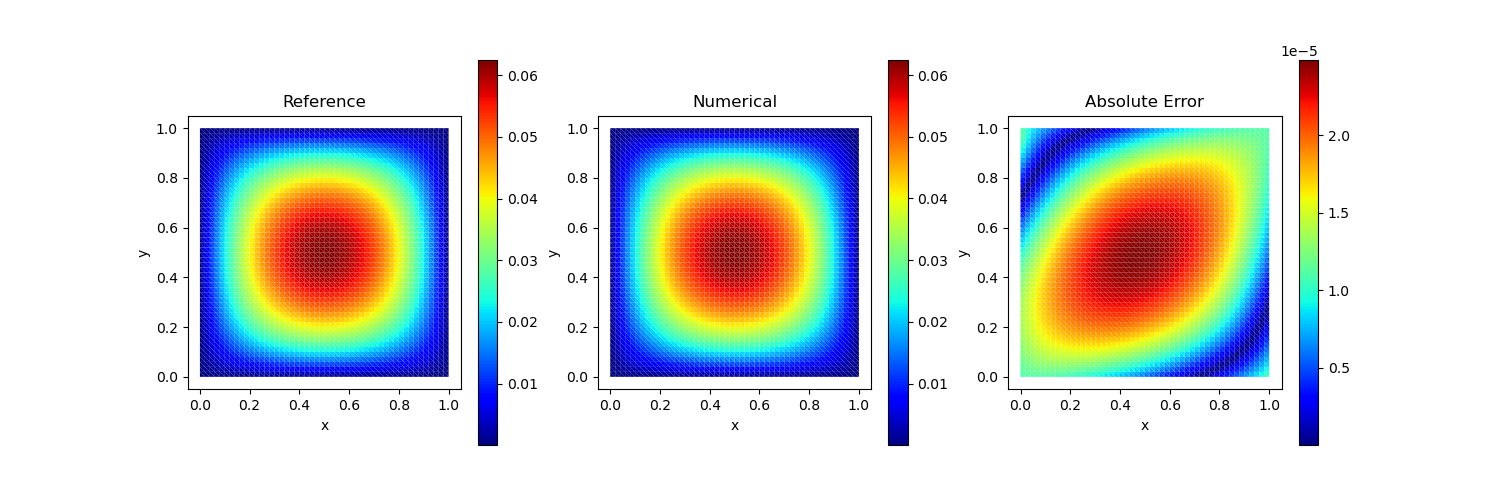
Test Case 1
Analytical solution:
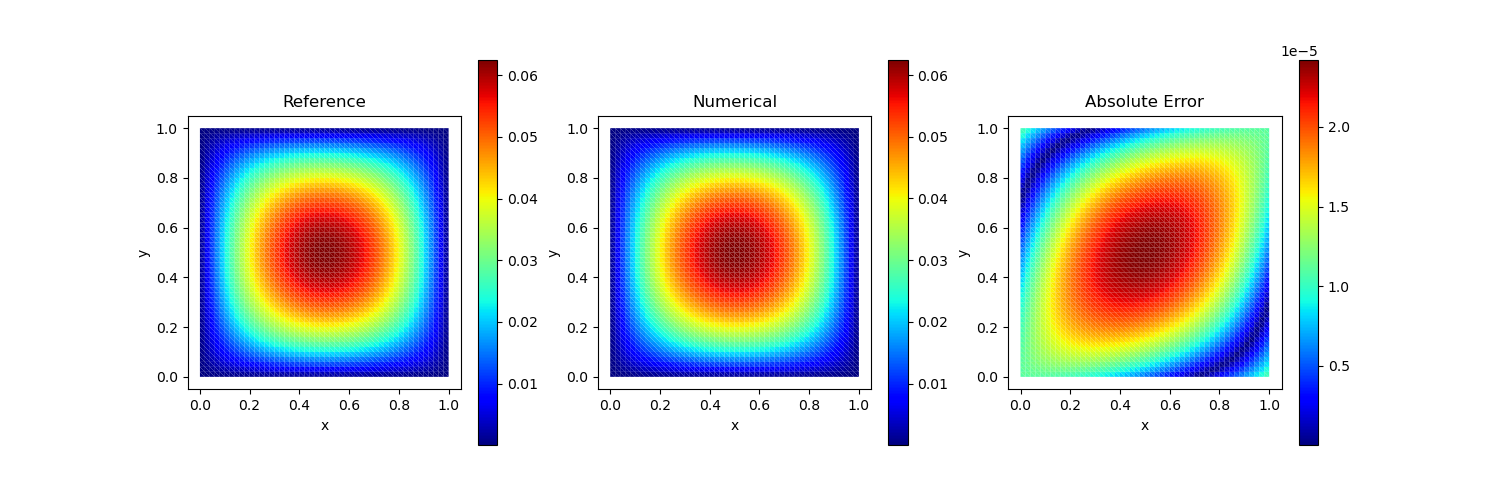
Test Case 2
Analytical solution:
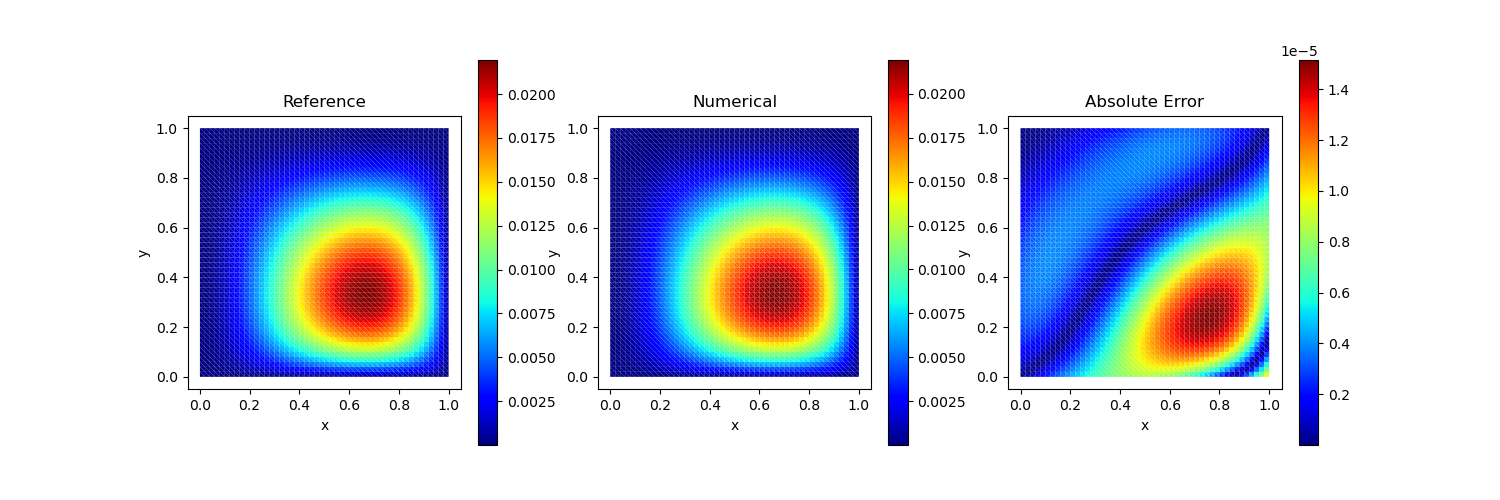
Test Case 3
Analytical solution:
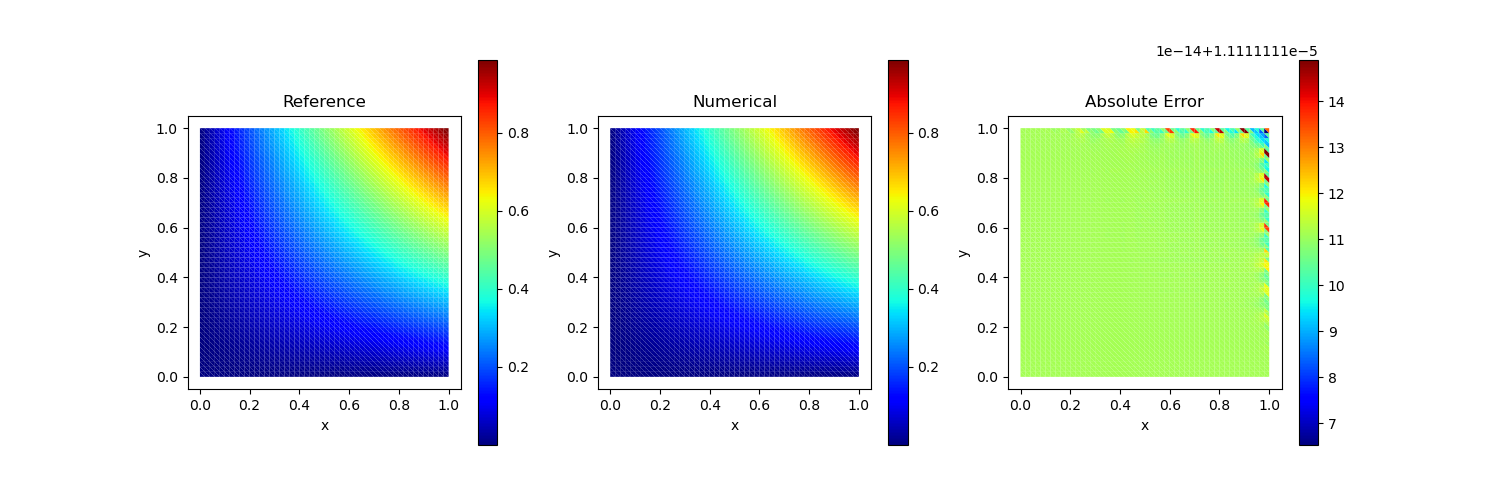
Test Case 4
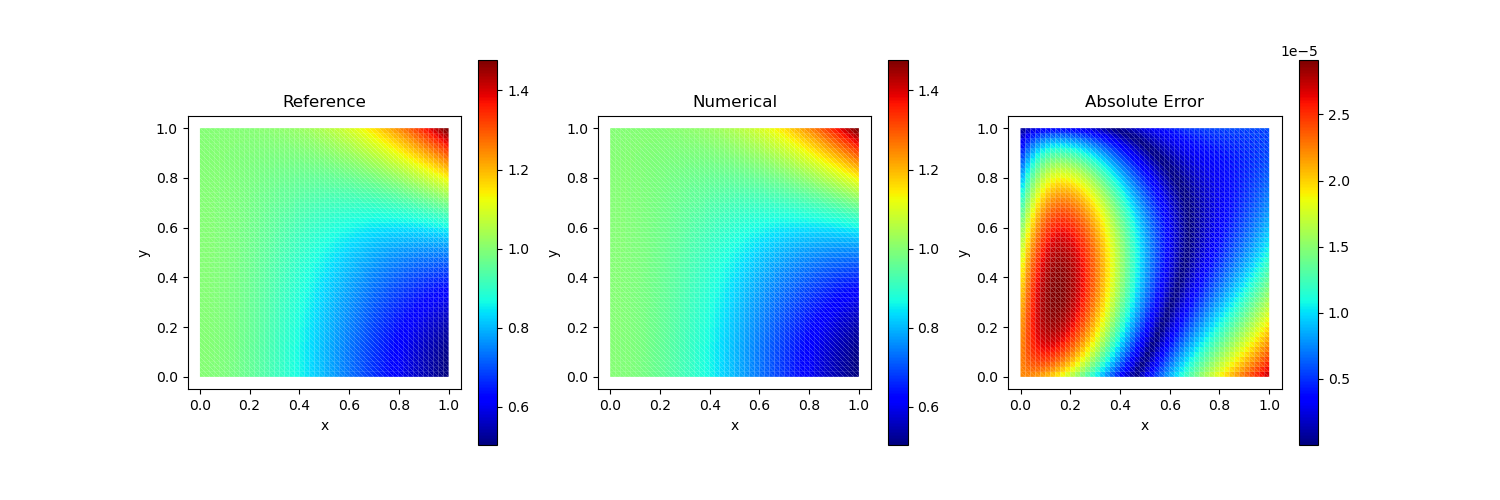
Traction Boundary Condition
We consider the case where the boundary conditions are given by
The weak form is
In this case, the traction boundary condition does not appear in the weak form, but determines the coefficients for the representation of $\sigma$ for the DOFs on the boundary $\Gamma_N$. Consider an edge $E_l = \{e_s, e_t\}, s<t$, then we have
which leads to
To calculate $a, b$, we solve the following linear system
The boundary condition can be computed using impose_bdm_traction_boundary_condition1.
# Solves the Poisson equation using the Mixed finite element method
using Revise
using AdFem
using DelimitedFiles
using SparseArrays
using PyPlot
n = 50
mmesh = Mesh(n, n, 1/n, degree = BDM1)
function ufunc(x, y)
x * (1-x) * y * (1-y)
end
function ffunc(x, y)
-2x*(1-x) -2y*(1-y)
end
function gfunc(x, y)
(1-2x)*y*(1-y)
end
A = compute_fem_bdm_mass_matrix1(mmesh)
B = compute_fem_bdm_div_matrix1(mmesh)
C = [A -B'
-B spzeros(mmesh.nelem, mmesh.nelem)]
gD = (x1, y1, x2, y2)->!( (x1<1e-3 && y1>1e-3 && y1<1-1e-3) || (x2<1e-3 && y2>1e-3 && y2<1-1e-3))
gN = (x1, y1, x2, y2)->x1<1e-5 && x2<1e-5
D_bdedge = bcedge(gD, mmesh)
N_bdedge = bcedge(gN, mmesh)
t1 = eval_f_on_boundary_edge(ufunc, D_bdedge, mmesh)
g = compute_fem_traction_term1(t1, D_bdedge, mmesh)
t2 = eval_f_on_gauss_pts(ffunc, mmesh)
f = compute_fvm_source_term(t2, mmesh)
gN = eval_f_on_boundary_edge(gfunc, N_bdedge, mmesh)
dof, val = impose_bdm_traction_boundary_condition1(gN, N_bdedge, mmesh)
rhs = [-g; f]
C, rhs = impose_Dirichlet_boundary_conditions(C, rhs, dof, val)
sol = C\rhs
u = sol[mmesh.ndof+1:end]
close("all")
figure(figsize=(15, 5))
subplot(131)
title("Reference")
xy = fvm_nodes(mmesh)
x, y = xy[:,1], xy[:,2]
uf = ufunc.(x, y)
visualize_scalar_on_fvm_points(uf, mmesh)
subplot(132)
title("Numerical")
visualize_scalar_on_fvm_points(u, mmesh)
subplot(133)
title("Absolute Error")
visualize_scalar_on_fvm_points( abs.(u - uf) , mmesh)
savefig("mixed_poisson_neumann.png")The result is shown below