Long Duration Storage for Hydrogen

h2_long_duration_storage(EP::Model, inputs::Dict)

Sets up variables and constraints common to all long duration hydrogen storage resources.

This function creates variables and constraints enabling modeling of long duration hydrogen storage resources when modeling representative time periods.

Long duration hydrogen storage initial inventory and change decision variables

This module defines the initial storage hydrogen inventory level variable $U_{s,z,t}^{\textrm{H,STO}} \forall s \in \mathcal{S}, z \in \mathcal{Z}, t \in \mathcal{T}_{p}^{start}$, representing initial hydrogen stored in the storage device $s$ in zone $z$ at all starting time period $t$ of modeled periods.

This module defines the change of storage hydrogen inventory level during each representative period $\Delta U_{s,z,m}^{\textrm{H,STO}} \forall s \in \mathcal{S}, z \in \mathcal{Z}, m \in \mathcal{M}$, representing the change of storage hydrogen inventory level of the storage device $s$ in zone $z$ during each representative period $m$.

The variable defined in this file named after vH2SOCw covers $U_{s,z,t}^{\textrm{H,STO}} \forall s \in \mathcal{S}, z \in \mathcal{Z}, t \in t \in \mathcal{T}_{p}^{start}$.

The variable defined in this file named after vdH2SOC covers $\Delta U_{s,z,m}^{\textrm{H,STO}} \forall s \in \mathcal{S}, z \in \mathcal{Z}, m \in \mathcal{M}$.

Storage inventory balance at beginning of each representative period

The constraints in this section are used to approximate the behavior of long-duration hydrogen storage technologies when approximating annual grid operations by modeling operations over representative periods. Previously, the state of charge balance for storage (as defined in storage_all()) assumed that state of charge at the beginning and end of each representative period has to be the same. In other words, the amount of hydrogen built up or consumed by storage technology $s$ in zone $z$ over the representative period $m$, $\Delta U_{s,z,m}^{\textrm{H,STO}} = 0$. This assumption implicitly excludes the possibility of transferring hydrogen from one representative period to the other which could be cost-optimal when the capital cost of hydrogen storage capacity is relatively small. To model long-duration hydrogen storage using representative periods, we replace the state of charge equation, such that the first term on the right hand side accounts for change in hydrogen storage inventory associated with representative period $m$ ($\Delta U_{s,z,m}^{\textrm{H,STO}}$), which could be positive (net accumulation) or negative (net reduction).

\[\begin{equation*} U_{s,z,(m-1)\times\tau^{period}+1}^{\textrm{H,STO}} = \left(1-\eta_{s,z}^{\textrm{H,STO,loss}}\right) \times \left(U_{s,z,m\times \tau^{period}} - \Delta U_{s,z,m}\right) - \frac{1}{\eta_{s,z}^{\textrm{\textrm{H,STO,DIS}}}}x_{s,z,(m-1)\times \tau^{period}+1}^{\textrm{H,STO}} + \eta_{s,z}^{\textrm{H,STO,CHA}}x_{s,z,(m-1)\times \tau^{period}+1}^{\textrm{H,STO}} \quad \quad \forall s \in \mathcal{S}^{LDES}, z \in \mathcal{Z}, m \in \mathcal{M} \end{equation*}\]

By definition $\mathcal{T}^{start}=\{\left(m-1\right) \times \tau^{period}+1 | m \in \mathcal{M}\}$, which implies that this constraint is defined for all values of $t \in T^{start}$.

Hydrogen storage inventory change input periods

We need additional variables and constraints to approximate hydrogen exchange between representative periods, while accounting for their chronological occurence in the original input time series data and the possibility that two representative periods may not be adjacent to each other (see Figure below). To implement this, we introduce a new variable $U_{s,z,n}$ that models inventory of storage technology $s \in \mathcal{S}$ in zone $z$ in each input period $n \in \mathcal{N}$. Additionally we define a function mapping, $f: n \rightarrow m$, that uniquely maps each input period $n$ to its corresponding representative period $m$. This mapping is available as an output of the process used to identify representative periods (E.g. k-means clustering Mallapragada et al., 2018).

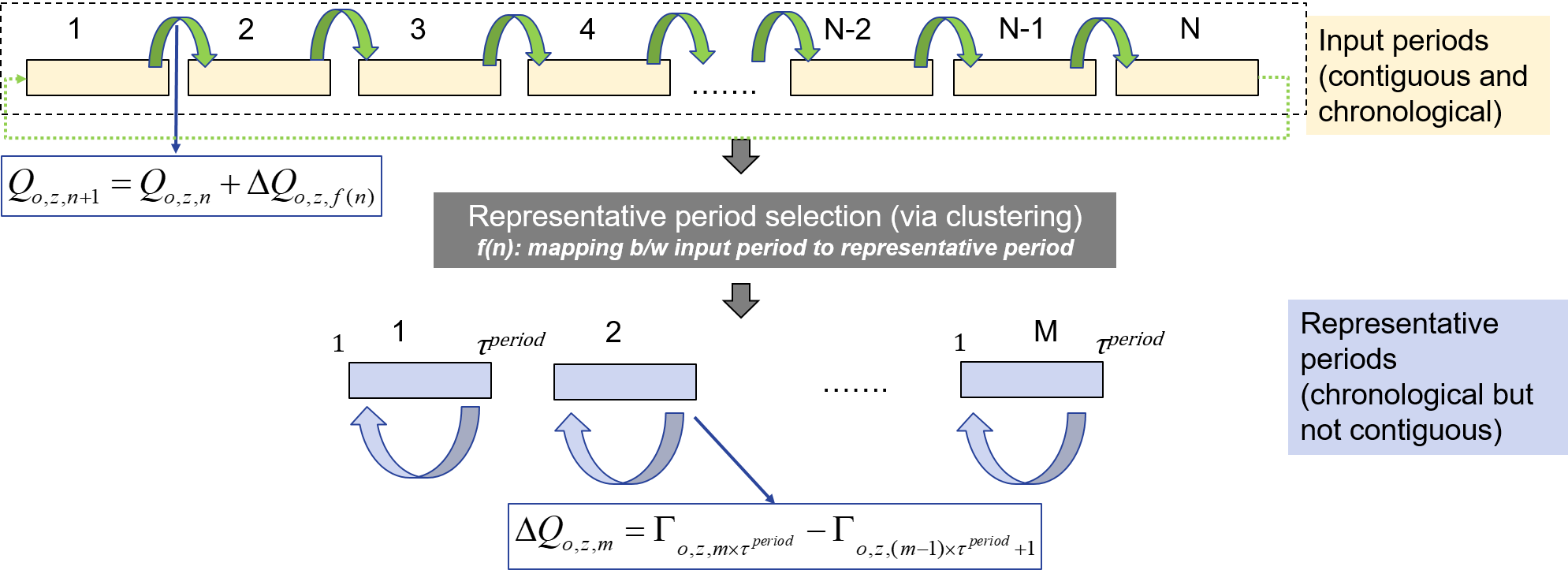Figure. Modeling inter-period hydrogen exchange via long-duration storage when using representative period temporal resolution to approximate annual grid operations

The following two equations define the hydrogen storage inventory at the beginning of each input period $n+1$ as the sum of storage inventory at begining of previous input period $n$ plus change in storage inventory for that period. The latter is approximated by the change in storage inventory in the corresponding representative period, identified per the mapping $f(n)$. The second constraint relates the storage level of the last input period, $|N|$, with the storage level at the beginning of the first input period. Finally, if the input period is also a representative period, then a third constraint enforces that initial storage level estimated by the intra-period storage balance constraint should equal the initial storage level estimated from the inter-period storage balance constraints. Note that $|N|$ refers to the last modeled period.

\[\begin{equation*} U_{s,z,n+1}^{\textrm{H,STO}} = U_{s,z,n}^{\textrm{H,STO}} + \Delta U_{s,z,f(n)} \quad \forall s \in \mathcal{S}^{LDES}, z \in \mathcal{Z}, n \in \mathcal{N}\setminus\{|N|\} \end{equation*}\]

\[\begin{equation*} U_{s,z,1}^{\textrm{H,STO}} = U_{s,z,|N|}^{\textrm{H,STO}} + \Delta U_{s,z,f(|N|)}^{\textrm{H,STO}} \quad \forall s \in \mathcal{S}^{LDES}, z \in \mathcal{Z}, n = |N| \end{equation*}\]

\[\begin{equation*} U_{s,z,n}^{\textrm{H,STO}} = U_{s,z,f(n) \times \tau^{period}}^{\textrm{H,STO}} - \Delta U_{s,z,m}^{\textrm{H,STO}} \quad \forall s \in \mathcal{S}^{LDES}, z \in \mathcal{Z}, n \in \mathcal{N}^{rep}, \end{equation*}\]

Finally, the next constraint enforces that the initial storage level for each input period $n$ must be less than the installed energy capacity limit. This constraint ensures that installed energy storage capacity is consistent with the state of charge during both the operational time periods $t$ during each sample period $m$ as well as at the start of each chronologically ordered input period $n$ in the full annual time series.

\[\begin{equation*} U_{s,z,n}^{\textrm{H,STO}} \leq y_{s,z}^{\textrm{H,STO,ENE}} \quad \forall s \in \mathcal{S}^{LDES}, z \in \mathcal{Z}, n \in \mathcal{N} \end{equation*}\]